Johnson Unbounded Distribution (JohnsonSU) :: SAS(R) Simulation Studio 12.3: User's Guide

Johnson Unbounded Distribution (JohnsonSU)

The density function of the Johnson unbounded distribution (JohnsonSU) is

$f(x) = \frac{\delta }{\lambda \sqrt {2\pi }}g’\left(\frac{x - \xi }{\lambda }\right)\mbox{exp}\left(-\frac{1}{2}\left[\gamma + \delta g\left(\frac{x - \xi }{\lambda }\right)\right]^2\right)$

where

$\begin{array}{l} g(y) = \mbox{ln}\left[y + \sqrt {y^2 + 1}\right]\\ g’(y) = \frac{1}{\sqrt {y^2 + 1}} \end{array}$

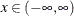and $x \in (-\infty , \infty )$ .

Parameters:

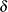$\delta$ (delta)	is a shape parameter, 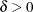$\delta > 0$ .
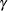$\gamma$ (gamma)	is a shape parameter.
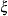$\xi$ (xi)	is the location parameter.
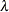$\lambda$ (lambda)	is the scale parameter, 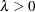$\lambda > 0$ .

Previous Page
|
Next Page
|
Top of Page