Johnson Bounded Distribution (JohnsonSB) :: SAS(R) Simulation Studio 12.3: User's Guide

Johnson Bounded Distribution (JohnsonSB)

The density function of the Johnson bounded distribution (JohnsonSB) is

$f(x) = \frac{\delta }{\lambda \sqrt {2\pi }}g’\left(\frac{x - \xi }{\lambda }\right)\mbox{exp}\left(-\frac{1}{2}\left[\gamma + \delta g\left(\frac{x - \xi }{\lambda }\right)\right]^2\right)$

where

$\begin{array}{l} g(y) = \mbox{ln}\left(\frac{y}{1 - y}\right)\\ g’(y) = \frac{1}{y(1 - y)} \end{array}$

and $x \in [\xi , \xi + \lambda ]$ .

Parameters:

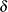$\delta$ (delta)	is a shape parameter, 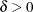$\delta > 0$ .
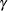$\gamma$ (gamma)	is a shape parameter.
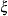$\xi$ (xi)	is the location parameter.
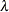$\lambda$ (lambda)	is the scale parameter, 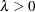$\lambda > 0$ .

Previous Page
|
Next Page
|
Top of Page