Negative Binomial :: SAS(R) Simulation Studio 12.3: User's Guide

The probability mass function of the negative binomial distribution is

$p(x) = \frac{(n + x - 1)!}{x!(n - 1)!}p^{n}(1 - p)^{x}$

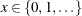for $x \in \{ 0, 1, \dots \}$ .

Parameters:

	is a positive integer $\ge$ 1 which represents the number
	of successes in a series of independent Bernoulli trials.
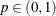
$p \in (0, 1)$	is the probability of success on each trial.