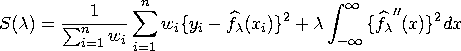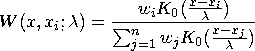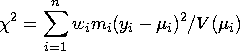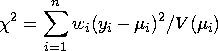Fit Analyses

Weighted Analyses

If the errors $\varepsilon_{i}$ do not have a common variance in the regression model

$y_{i} = f( x_{i}) + \varepsilon_{i}$

a weighted analysis may be appropriate. The observation weights are the values of the Weight variable you specified.

In parametric regression, the linear model is given by

$y = X {\beta} + {{\epsilon}}$

Let W be an n×n diagonal matrix consisting of weights w₁>0, w₂>0, ..., and w_n>0 for the observations, and let W^1/2 be an n×n diagonal matrix with diagonal elements w₁^1/2, w₂^1/2, ..., and w_n^1/2.

The weighted fit analysis is equivalent to the usual (unweighted) fit analysis of the transformed model

$y^{{\ast}} = X^{{\ast}} {\beta} + {\epsilon}^{{\ast}}$

where ${ y^{{\ast}} = W^{1/2} y}$ , ${ X^{{\ast}} = W^{1/2} X}$ , and ${ {\epsilon}^{{\ast}} = W^{1/2} {\epsilon}}$ .

The estimate of $\beta$ is then given by

b_w = (X'WX)^-1 X'Wy

For nonparametric weighted regression, the minimizing criterion in spline estimation is given by

$S(\lambda) = \frac{1}{\sum_{i=1}^n{w_{i}}} \sum_{i=1}^n{w_{i} \{ y_{i} - \hat... ... \}^2} + \lambda \int_{-{\infty}}^{{\infty}}{\{ {\hat{f_\lambda}"}(x) \}^2 dx}$

In kernel estimation, individual weights are

$W(x, x_{i};\lambda) = \frac{w_{i} K_{0}(\frac{x- x_{i}}{\lambda})}{\sum_{j=1}^n{w_{j} K_{0}(\frac{x- x_{j}}{\lambda})} }$

For generalized linear models, the function ${ a_{i}(\phi) = \phi / ( m_{i} w_{i})}$ for binomial distribution with m_i trials in the ith observation, ${ a_{i}(\phi) = \phi / w_{i}}$ for other distributions. The function ${ a_{i}(\phi)}$ is used to compute the likelihood function and the diagonal matrices W_o and W_e.

The individual deviance contribution d_i is obtained by multiplying the weight w_i by the unweighted deviance contribution. The deviance is the sum of these weighted deviance contributions.

The Pearson $\chi^2$ statistic is

$\chi^2 = \sum_{i=1}^n{w_{i} m_{i} ( y_{i}- \mu_{i})^2 / V( \mu_{i}) }$

for binomial distribution with m_i trials in the ith observation,

$\chi^2 = \sum_{i=1}^n{w_{i} ( y_{i}- \mu_{i})^2 / V( \mu_{i}) }$

for other distributions.

Top of Page