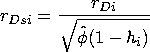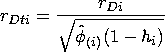Deviance Residuals

Fit Analyses

Deviance Residuals

The deviance residual is the measure of deviance contributed from each observation and is given by

$r_{Di} = \rm{sign}( r_{i}) \sqrt{ d_{i}}$

where d_i is the individual deviance contribution.

The deviance residuals can be used to check the model fit at each observation for generalized linear models. These residuals are stored in variables named RD_yname for each response variable, where yname is the response variable name.

The standardized and studentized deviance residuals are

$r_{Dsi} = \frac{r_{Di}}{\sqrt{\hat{ \phi} (1- h_{i})} }$

$r_{Dti} = \frac{r_{Di}}{\sqrt{ \hat{ \phi}_{(i)} (1- h_{i})}}$

The standardized deviance residuals are stored in variables named RDS_yname and the studentized deviance residuals are stored in variables named RDT_yname for each response variable, where yname is the response variable name.

Top of Page