The SHEWHART Procedure

The next step is to model the trend as a function of hour. The 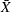chart in Figure 18.165 suggests that the mean level of the process (saved as DiameterX in the OUTLIMITS= data set submeans) grows as the log of hour. The following statements fit a simple linear regression model in which DiameterX is the response variable and loghour (the log transformation of hour) is the predictor variable. Part of the printed output produced by PROC REG is shown in Figure 18.166.

data submeans;
   set submeans;
   loghour=log(hour);
run;

proc reg data=submeans ;
   model Diameterx=loghour;
   output out=regdata predicted=fitted ;
run;

Figure 18.166 shows that the fitted equation can be expressed as

where 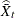is the fitted subgroup average.^[39] A partial listing of the OUT= data set REGDATA created by the REG procedure is shown in Figure 18.167.