The OPTEX Procedure

CLASS Statement

  • CLASS variable <(v-options)> <variable <(v-options)> …> </ v-options>>;

You use the CLASS statement to identify classification (qualitative) variables, which are factors that separate the observations into groups. For example, a completely randomized design has a single class-variable that identifies the groups of observations. A randomized complete block design has two class-variables; one identifies the blocks and one identifies the treatments.

You can specify various v-options for each variable by enclosing them in parentheses after the variable name. You can also specify global v-options for the CLASS statement by placing them after a slash (/). Global v-options are applied to all the variables specified in the CLASS statement. However, individual CLASS variable v-options override the global v-options.

Class-variables can be either numeric or character. The OPTEX procedure uses the formatted values of class-variables in forming model effects. Any variable in the model that is not listed in the CLASS statement is assumed to be continuous (quantitative). Continuous variables must be numeric.

Note: If you specify a data set containing fixed covariate effects with a DESIGN= data set in the BLOCKS statement, then a CLASS or MODEL statement that follows the BLOCKS statement refers to the model for the fixed covariates. A CLASS or MODEL statement that defines the model for the candidate points (treatment model) should be specified before the BLOCKS statement.

DESCENDING
DESC

reverses the sorting order of the classification variable.

ORDER=DATA | FORMATTED | FREQ | INTERNAL

specifies the sorting order for the levels of classification variables. This ordering determines which parameters in the model correspond to each level in the data, so the ORDER= option may be useful when you use the CONTRAST statement. When ORDER=FORMATTED (the default) for numeric variables for which you have supplied no explicit format (that is, for which there is no corresponding FORMAT statement in the current PROC OPTEX run or in the DATA step that created the data set), the levels are ordered by their internal (numeric) value. Note that this represents a change from previous releases for how class levels are ordered. Before SAS 8, numeric class levels with no explicit format were ordered by their BEST12. formatted values, and in order to revert to the previous ordering you can specify this format explicitly for the affected classification variables. The change was implemented because the former default behavior for ORDER=FORMATTED often resulted in levels not being ordered numerically. The following table shows how PROC OPTEX interprets values of the ORDER= option.

Value of ORDER=

Levels Sorted By

DATA

order of appearance in the input data set

FORMATTED

external formatted value, except for numeric

 

variables with no explicit format, which are

 

sorted by their unformatted (internal) value

FREQ

descending frequency count; levels with the

 

most observations come first in the order

INTERNAL

unformatted value

By default, ORDER=FORMATTED. For FORMATTED and INTERNAL, the sort order is machine dependent.

For more information on sorting order, see the chapter on the SORT procedure in the Base SAS Procedures Guide and the discussion of BY-group processing in SAS Language Reference: Concepts.

PARAM=keyword

specifies the parameterization method for the classification variable(s). Design matrix columns are created from CLASS variables according to the following coding schemes. The default is PARAM=ORTHEFFECT. Note that this represents a change from previous releases for how classification variables are parameterized. Before SAS 9, the default was PARAM=EFFECT, and in order to revert to the previous parameterization you can specify PARAM=EFFECT explicitly for the affected classification variables. The change was implemented because an orthogonal parameterization leads to D- and A-efficiency values that more realistically reflect the true efficiency of the design. If PARAM=ORTHPOLY or PARAM=POLY, and the CLASS levels are numeric, then the ORDER= option in the CLASS statement is ignored, and the internal, unformatted values are used.

EFFECT

specifies effect coding

POLYNOMIAL  |  POLY

specifies polynomial coding

REFERENCE  |  REF

specifies reference cell coding

ORDINAL  |  ORD

specifies ordinal, or "thermometer" coding

ORTHEFFECT

specifies orthogonal effect coding

ORTHPOLY

specifies orthogonal polynomial coding

ORTHREF

specifies orthogonal reference cell coding

ORTHORDINAL

specifies orthogonal ordinal coding

All of these parameterizations are full rank. The orthogonal versions perform a scaled, intercept-augmented Gram-Schmidt orthogonalization on the columns of the corresponding nonorthogonal parameterizations. For the EFFECT and REFERENCE parameterizations, the REF= option in the CLASS statement determines the reference level.

Consider a model with one CLASS variable A with four levels, 1, 2, 5, and 7. Details of the possible choices for the PARAM= option follow.

EFFECT

Three columns are created to indicate group membership of the nonreference levels. For the reference level, all three dummy variables have a value of –1. For instance, if the reference level is 7 (REF=7), the design matrix columns for A are as follows.

Effect Coding

A

Design Matrix

1

1

0

0

2

0

1

0

5

0

0

1

7

–1

–1

–1

Parameter estimates of CLASS main effects that uses the effect coding scheme estimate the difference in the effect of each nonreference level compared to the average effect over all 4 levels.

POLYNOMIAL  |  POLY

Three columns are created. The first represents the linear term (x), the second represents the quadratic term (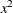$x^2$), and the third represents the cubic term (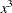$x^3$), where x is the level value. If the CLASS levels are not numeric, they are translated into 1, 2, 3, $\dots $ according to their sorting order. The design matrix columns for A are as follows.

Polynomial Coding

A

Design Matrix

1

1

1

1

2

2

4

8

5

5

25

125

7

7

49

343

REFERENCE  |  REF

Three columns are created to indicate group membership of the nonreference levels. For the reference level, all three dummy variables have a value of 0. For instance, if the reference level is 7 (REF=7), the design matrix columns for A are as follows.

Reference Coding

A

Design Matrix

1

1

0

0

2

0

1

0

5

0

0

1

7

0

0

0

Parameter estimates of CLASS main effects that uses the reference coding scheme estimate the difference in the effect of each nonreference level compared to the effect of the reference level.

ORDINAL  |  ORD

Three columns are created to indicate group membership in successive collections of levels after the first. For instance, the design matrix columns for A are as follows.

Ordinal Coding

A

Design Matrix

1

0

0

0

2

1

0

0

5

1

1

0

7

1

1

1

Parameter estimates of CLASS main effects that uses the ordinal coding scheme estimate the difference in the average effect of each successive collection of levels compared to the effect of the first level.

ORTHEFFECT

The columns are obtained by applying the Gram-Schmidt orthogonalization to the mean-centered columns for PARAM=EFFECT, and then scaling so that the sum of squares for each column equals the number of levels. The design matrix columns for A are as follows.

Orthogonal Effects Coding

A

Design Matrix

1

1.414

–0.816

–0.577

2

0

1.633

–0.577

5

0

0

1.732

7

–1.414

–0.816

–0.577

ORTHPOLY

The columns are obtained by applying the Gram-Schmidt orthogonalization to the mean-centered columns for PARAM=POLY, and then scaling so that the sum of squares for each column equals the number of levels. The design matrix columns for A are as follows.

Orthogonal Polynomial Coding

A

Design Matrix

1

–1.153

0.907

–0.921

2

–0.734

–0.540

1.473

5

0.524

–1.370

–0.921

7

1.363

1.004

0.368

ORTHREF

The columns are obtained by applying the Gram-Schmidt orthogonalization to the mean-centered columns for PARAM=REFERENCE, and then scaling so that the sum of squares for each column equals the number of levels. The design matrix columns for A are as follows.

Orthogonal Reference Coding

A

Design Matrix

1

1.732

0

0

2

–0.577

1.633

0

5

–0.577

–0.816

1.414

7

–0.577

–0.816

–1.414

ORTHORDINAL

The columns are obtained by applying the Gram-Schmidt orthogonalization to the mean-centered columns for PARAM=REFERENCE, and then scaling so that the sum of squares for each column equals the number of levels. The design matrix columns for A are as follows.

Orthogonal Ordinal Coding

A

Design Matrix

1

–1.732

0

0

2

0.577

–1.633

0

5

0.577

0.816

–1.414

7

0.577

0.816

1.414

REF=’level’ | keyword

specifies the reference level for PARAM=EFFECT or PARAM=REFERENCE. For an individual (but not a global) variable REF= option, you can specify the level of the variable to use as the reference level. For a global or individual variable REF= option, you can use one of the following keywords. The default is REF=LAST.

FIRST

designates the first ordered level as reference

LAST

designates the last ordered level as reference

TRUNCATE

specifies that class levels should be determined by using only up to the first 16 characters of the formatted values of CLASS variables. When formatted values are longer than 16 characters, you can use this option in order to revert to the levels as determined in releases previous to SAS 9.