Functions

PROBMED Function

Subsections:

computes cumulative probabilities for the sample median.

Syntax

PROBMED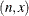$(n,x)$

where

n

is the sample size.

x

is the point of interest; that is, the PROBMED function calculates the probability that the median is less than or equal to x.

Description

The PROBMED function computes the probability that the sample median is less than or equal to x for a sample of n independent, standard normal random variables (mean 0, variance 1).

Let n represent the sample size and 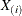$X_{(i)}$ represent the ith order statistic. Then, when n is odd, the function calculates

\[ \Pr [X_{((n+1)/2)}\leq x] = \mbox{I}_{\Phi (x)} \left( \frac{n+1}{2}, \frac{n+1}{2} \right) \]

where

\[ \mbox{I}_ p(a,b) = \frac{1}{\mbox{B}(a,b) } \displaystyle \int _0^ p t^{a-1}(1-t)^{b-1}\, dt \]

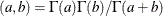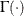and B$(a,b) = \Gamma (a)\Gamma (b)/\Gamma (a+b)$, where $\Gamma (\cdot )$ is the gamma function. If n is even, the PROBMED function calculates

\[ \mbox{Pr} \left[ \frac{ X_{(n/2)} + X_{((n/2)+1)} }{2} \leq x \right] = \]
\[ \mbox{} \frac{2}{ \mbox{B}(\frac{n}{2},\frac{n}{2}) } {\displaystyle \int _{-\infty }^ x} \left\{ [1-\Phi (u)]^{n/2}-[1-\Phi (2x-u)]^{n/2} \right\} [\Phi (u)]^{(n/2)-1} \, \phi (u) \, du \]

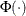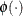where B$(n/2,n/2) = [\Gamma (n/2)]^2/ \Gamma (n) $ and $\Phi (\cdot )$ and $\phi (\cdot )$ are the standard normal cumulative distribution function and density function, respectively.

For more information, refer to David (1981).

Examples

The statements 

data;
   b=probmed(5,-0.1);
   put b;
run;

result in a value of 0.4256380897.