The FACTEX Procedure
Example 7.18 Design and Analysis of a Complete Factorial Experiment
Note: See Complete Factorial Experiment in the SAS/QC Sample Library.
Yin and Jillie (1987) describe an experiment on a nitride etch process for a single-wafer plasma etcher. The experiment has four factors: cathode
power (Power), gas flow (Flow), reactor chamber pressure (Pressure), and electrode gap (Gap). A single replicate of a 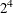 design is run, and the etch rate (
design is run, and the etch rate (Rate) is measured.
You can use the following statements to construct a 16-run design in the four factors:
proc factex;
factors Power Flow Pressure Gap;
output out=EtcherDesign
Power nvals=(0.80 1.20)
Flow nvals=(4.50 550)
Pressure nvals=(125 200)
Gap nvals=(275 325);
run;
The design with the actual (decoded) factor levels is saved in the data set EtcherDesign. The experiment that uses the 16-run design is performed, and the etch rate is measured. The following DATA step updates
the data set EtcherDesign with the values of Rate:
data EtcherDesign; set EtcherDesign; input Rate @@; datalines; 550 669 604 650 633 642 601 635 1037 749 1052 868 1075 860 1063 729 ;
title 'Nitride Etch Process Experiment'; proc print; run;
The data set DESGNDAT is listed in Output 7.18.1.
Output 7.18.1: A 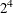 Design with Responses
Design with Responses
| Nitride Etch Process Experiment |
| Obs | Power | Flow | Pressure | Gap | Rate |
|---|---|---|---|---|---|
| 1 | 0.8 | 4.5 | 125 | 275 | 550 |
| 2 | 0.8 | 4.5 | 125 | 325 | 669 |
| 3 | 0.8 | 4.5 | 200 | 275 | 604 |
| 4 | 0.8 | 4.5 | 200 | 325 | 650 |
| 5 | 0.8 | 550.0 | 125 | 275 | 633 |
| 6 | 0.8 | 550.0 | 125 | 325 | 642 |
| 7 | 0.8 | 550.0 | 200 | 275 | 601 |
| 8 | 0.8 | 550.0 | 200 | 325 | 635 |
| 9 | 1.2 | 4.5 | 125 | 275 | 1037 |
| 10 | 1.2 | 4.5 | 125 | 325 | 749 |
| 11 | 1.2 | 4.5 | 200 | 275 | 1052 |
| 12 | 1.2 | 4.5 | 200 | 325 | 868 |
| 13 | 1.2 | 550.0 | 125 | 275 | 1075 |
| 14 | 1.2 | 550.0 | 125 | 325 | 860 |
| 15 | 1.2 | 550.0 | 200 | 275 | 1063 |
| 16 | 1.2 | 550.0 | 200 | 325 | 729 |
To perform an analysis of variance on the responses, you can use the GLM procedure, as follows:
proc glm data=EtcherDesign; class Power Flow Pressure Gap; model rate=Power|Flow|Pressure|Gap@2 / ss1; run;
The factors are listed in both the CLASS and MODEL statements, and the response as a function of the factors is modeled by using the MODEL statement. The MODEL statement requests Type I sum of squares (SS1) and lists all effects that contain two or fewer factors. It is assumed that three-factor and higher interactions are not significant.
Part of the output from the GLM procedure is shown in Output 7.18.2. The main effect of the factors Power and Gap and the interaction between Power and Gap are significant (their p-values are less than 0.01).
Output 7.18.2: Analysis of Variance for the Nitride Etch Process Experiment
| Nitride Etch Process Experiment |
| Source | DF | Type I SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Power | 1 | 374850.0625 | 374850.0625 | 183.99 | <.0001 |
| Flow | 1 | 217.5625 | 217.5625 | 0.11 | 0.7571 |
| Power*Flow | 1 | 18.0625 | 18.0625 | 0.01 | 0.9286 |
| Pressure | 1 | 10.5625 | 10.5625 | 0.01 | 0.9454 |
| Power*Pressure | 1 | 1.5625 | 1.5625 | 0.00 | 0.9790 |
| Flow*Pressure | 1 | 7700.0625 | 7700.0625 | 3.78 | 0.1095 |
| Gap | 1 | 41310.5625 | 41310.5625 | 20.28 | 0.0064 |
| Power*Gap | 1 | 94402.5625 | 94402.5625 | 46.34 | 0.0010 |
| Flow*Gap | 1 | 2475.0625 | 2475.0625 | 1.21 | 0.3206 |
| Pressure*Gap | 1 | 248.0625 | 248.0625 | 0.12 | 0.7414 |