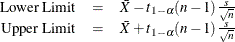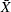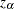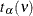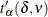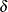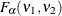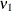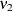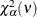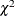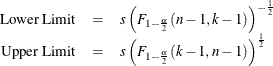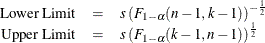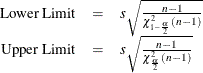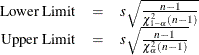The CAPABILITY Procedure

Methods for Computing Statistical Intervals

The formulas for statistical intervals given in this section use the following notation:

Notation

Definition

n

number of nonmissing values for a variable

$\bar{X}$

mean of variable

s

standard deviation of variable

$z_{\alpha }$

100$\alpha $th percentile of the standard normal distribution

$t_{\alpha }(\nu )$

100$\alpha $th percentile of the central t distribution with $\nu $ degrees of freedom

$t^{\prime }_{\alpha }(\delta ,\nu )$

100$\alpha $th percentile of the noncentral t distribution with noncentrality

 

parameter $\delta $ and $\nu $ degrees of freedom

$F_{\alpha }(\nu _1,\nu _2)$

100$\alpha $th percentile of the F distribution with $\nu _1$ degrees of freedom in

 

the numerator and $\nu _2$ degrees of freedom in the denominator

$\chi ^{2}_{\alpha }(\nu )$

100$\alpha $th percentile of the $\chi ^2$ distribution with $\nu $ degrees of freedom.

The values of the variable are assumed to be independent and normally distributed. The intervals are computed using the degrees of freedom as the divisor for the standard deviation s. This divisor corresponds to the default of VARDEF=DF in the PROC CAPABILITY statement. If you specify another value for the VARDEF= option, intervals are not computed.

You select the intervals to be computed with the METHODS= option. The next six sections give computational details for each of the METHODS= options.

METHODS=1

This requests an approximate simultaneous prediction interval for k future observations. Two-sided intervals are computed using the conservative approximations

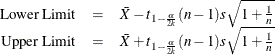
$ \begin{array}{rcl} \mbox{Lower Limit} & = & \bar{X} - t_{1- \frac{\alpha }{2k}} (n - 1) s \sqrt {1 + \frac{1}{n}} \\ \mbox{Upper Limit} & = & \bar{X} + t_{1- \frac{\alpha }{2k}} (n - 1) s \sqrt {1 + \frac{1}{n}} \end{array} $

One-sided limits are computed using the conservative approximation

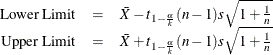
$ \begin{array}{rcl} \mbox{Lower Limit} & = & \bar{X} - t_{1- \frac{\alpha }{k}} (n - 1) s \sqrt {1 + \frac{1}{n}} \\ \mbox{Upper Limit} & = & \bar{X} + t_{1- \frac{\alpha }{k}} (n - 1) s \sqrt {1 + \frac{1}{n}} \end{array} $

Hahn (1970c) states that these approximations are satisfactory except for combinations of small n, large k, and large $\alpha $. Refer also to Hahn (1969, 1970a) and Hahn and Meeker (1991).

METHODS=2

This requests a prediction interval for the mean of k future observations. Two-sided intervals are computed as

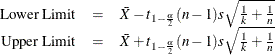
$ \begin{array}{rcl} \mbox{Lower Limit} & = & \bar{X} - t_{1-\frac{\alpha }{2}} (n - 1) s \sqrt {\frac{1}{k} + \frac{1}{n}} \\ \mbox{Upper Limit} & = & \bar{X} + t_{1- \frac{\alpha }{2}} (n - 1) s \sqrt {\frac{1}{k} + \frac{1}{n}} \end{array} $

One-sided limits are computed as

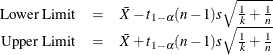
$ \begin{array}{rcl} \mbox{Lower Limit} & = & \bar{X} - t_{1-\alpha } (n - 1) s \sqrt {\frac{1}{k} + \frac{1}{n}} \\ \mbox{Upper Limit} & = & \bar{X} + t_{1-\alpha } (n - 1) s \sqrt {\frac{1}{k} + \frac{1}{n}} \end{array} $

METHODS=3

This requests an approximate statistical tolerance interval that contains at least proportion p of the population. Two-sided intervals are approximated by

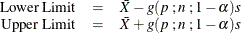
$ \begin{array}{rcl} \mbox{Lower Limit} & = & \bar{X} - g ( p~ ; n~ ; 1-\alpha ) s \\ \mbox{Upper Limit} & = & \bar{X} + g ( p~ ; n~ ; 1-\alpha ) s \end{array} $

where 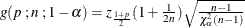$g(p~ ; n~ ; 1- \alpha )= z_{\frac{1+p}{2}}(1+\frac{1}{2n}) \sqrt {\frac{n - 1}{\chi ^2_{\alpha }(n - 1)}}$.

Exact one-sided limits are computed as

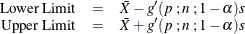
$ \begin{array}{rcl} \mbox{Lower Limit} & = & \bar{X} - g^{\prime }(p~ ; n~ ; 1- \alpha ) s \\ \mbox{Upper Limit} & = & \bar{X} + g^{\prime }(p~ ; n~ ; 1- \alpha ) s \end{array} $

where 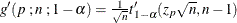$g^{\prime } (p~ ; n~ ; 1- \alpha ) = \frac{1}{\sqrt {n}} t^{\prime }_{1-\alpha }(z_ p \sqrt {n}, n - 1)$.

In some cases (for example, if 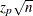$z_ p \sqrt {n}$ is large), 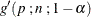$g^{\prime } (p~ ; n~ ; 1- \alpha )$ is approximated by

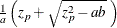
$ \frac{1}{a} \left(z_ p + \sqrt {z_ p^2 - ab}~ \right) $

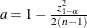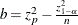where $a = 1 - \frac{z_{1-\alpha }^2}{2(n - 1)}$ and $b = z_ p^2 - \frac{z_{1-\alpha }^2}{n}$.

Hahn (1970b) states that this approximation is "poor for very small n, especially for large p and large 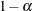$1-\alpha $, and is not advised for n < 8." Refer also to Hahn and Meeker (1991).

METHODS=4

This requests a confidence interval for the population mean. Two-sided intervals are computed as

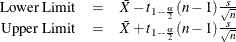
$ \begin{array}{rcl} \mbox{Lower Limit} & = & \bar{X} - t_{1-\frac{\alpha }{2}} (n - 1) \frac{s}{\sqrt {n}} \\ \mbox{Upper Limit} & = & \bar{X} + t_{1-\frac{\alpha }{2}} (n - 1) \frac{s}{\sqrt {n}} \end{array} $

One-sided limits are computed as

$ \begin{array}{rcl} \mbox{Lower Limit} & = & \bar{X} - t_{1-\alpha } (n - 1) \frac{s}{\sqrt {n}} \\ \mbox{Upper Limit} & = & \bar{X} + t_{1-\alpha } (n - 1) \frac{s}{\sqrt {n}} \end{array} $

METHODS=5

This requests a prediction interval for the standard deviation of k future observations. Two-sided intervals are computed as

$ \begin{array}{rcl} \mbox{Lower Limit} & = & s \left( F_{1-\frac{\alpha }{2}} (n - 1, k - 1) \right)^{-\frac{1}{2}} \\ \mbox{Upper Limit} & = & s \left( F_{1-\frac{\alpha }{2}} (k - 1, n - 1) \right)^{\frac{1}{2}} \end{array} $

One-sided limits are computed as

$ \begin{array}{rcl} \mbox{Lower Limit} & = & s \left( F_{1-\alpha } (n - 1, k - 1) \right)^{-\frac{1}{2}} \\ \mbox{Upper Limit} & = & s \left( F_{1-\alpha } (k - 1, n - 1) \right)^{\frac{1}{2}} \end{array} $

METHODS=6

This requests a confidence interval for the population standard deviation. Two-sided intervals are computed as

$ \begin{array}{rcl} \mbox{Lower Limit} & = & s \sqrt {\frac{n - 1}{\chi ^2_{1-\frac{\alpha }{2}} (n - 1)}} \\ \mbox{Upper Limit} & = & s \sqrt {\frac{n - 1}{\chi ^2_{\frac{\alpha }{2}} (n - 1)}} \\ \end{array} $

One-sided limits are computed as

$ \begin{array}{rcl} \mbox{Lower Limit} & = & s \sqrt {\frac{n - 1}{\chi ^2_{1-\alpha } (n - 1)}} \\ \mbox{Upper Limit} & = & s \sqrt {\frac{n - 1}{\chi ^2_{\alpha } (n - 1)}} \\ \end{array} $