Design Efficiency Measures :: SAS/QC(R) 13.1 User's Guide

Design Efficiency Measures

The output from the OPTEX procedure includes efficiency measures for the resulting designs according to various criteria. This section gives the precise definitions for these measures.

By default, the OPTEX procedure calculates the following efficiency measures for each design found in its search for an optimum design:

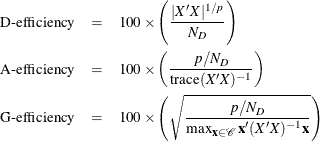
$\begin{eqnarray*} \mbox{D-efficiency} & =& 100\times \left( \frac{|XX|^{1/p}}{N_ D} \right) \\ \mbox{A-efficiency} & =& 100\times \left( \frac{p/N_ D}{\textrm{trace}(XX)^{-1}} \right) \\ \mbox{G-efficiency} & =& 100\times \left( \sqrt {\frac{p/N_ D}{\max _{\Strong{x}\in \mc {C}}\Strong{x}(XX)^{-1}\Strong{x}}} \right) \end{eqnarray*}$

where p is the number of parameters in the linear model, $N_ D$ is the number of design points, and $\mc {C}$ is the set of candidate points. The D- and A-efficiencies are the relative number of runs (expressed as percents) required by a hypothetical orthogonal design to achieve the same $|X’X|$ and $\mr {trace}(X’X)^{-1}$ , respectively; refer to Mitchell (1974b).

When you specify a BLOCKS statement, the D- and A-efficiencies for the treatment part of the model are calculated. These are calculated similarly to the preceding efficiencies, except that they are based on the information matrix after correcting for block/covariate effect(s). This matrix can be written as $X’A^{-1}X$ for a symmetric, positive definite matrix A that depends on the model for the block/covariate effect(s). If you specify a block structure or a covariate model, then $A=A^{-1}=I - Z(Z’Z)^{-1}Z’$ , where Z is the design matrix for the block/covariate effect(s). Alternatively, you can use the COVAR= option to specify the matrix A directly. Given A, the efficiencies in the presence of covariates are defined as follows:

$\begin{array}{rclrcl} \mbox{D-efficiency} & = & 100\times c_ D^{-1} \cdot |X’A^{-1}X|^{1/p} / N, & c_ D & = & \prod _{i=1}^ p \lambda _ i^{1/p} \\ \mbox{A-efficiency} & = & 100\times c_ A^{-1} \cdot (p/N)/\textrm{trace}(X’A^{-1}X)^{-1}, & c_ A & = & \sum _{i=1}^ p \lambda _ i /p \end{array}$

where $\lambda _1, \ldots , \lambda _ p$ are the p largest eigenvalues of $A^{-1}$ . If you use the STRUCTURE= block model specification and there is only one classification variable in the treatment model, then the design fits into the traditional block design framework. In this case, the D-efficiency relative to a balanced incomplete block design is also listed.

Because these efficiencies measure the goodness of the design relative to theoretical designs that might be far from possible in many cases, they are typically not useful as absolute measures of design goodness. Instead, efficiency measures should be used relatively, to compare one design to another for the same situation.

For the distance-based criteria, there are no simple measures of design efficiency that can be scaled from 0 to 100. See the section Output for a definition of the design measures tabulated for these criteria.