You can use the Base SAS functions PROBBNML and PROBHYPR to evaluate single-sampling plans. Measures of the performance of single-sampling plans include
-
the probability of acceptance
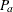
-
the average sample number ASN
-
the average outgoing quality AOQ
-
the average total inspection ATI
Since ![]() is the probability of finding c or fewer defectives in the sample, you can calculate the acceptance probability using the function PROBHYPR
is the probability of finding c or fewer defectives in the sample, you can calculate the acceptance probability using the function PROBHYPR![]() for Type A sampling and the function PROBBNML
for Type A sampling and the function PROBBNML![]() for Type B sampling.
for Type B sampling.
For example, the following statements calculate ![]() for the plan n = 20, c = 1 when sampling from a single lot of size N = 120 that contains D = 22 nonconforming items, resulting in a value of 0.0762970752:
for the plan n = 20, c = 1 when sampling from a single lot of size N = 120 that contains D = 22 nonconforming items, resulting in a value of 0.0762970752:
data; prob=probhypr(120,22,20,1); put prob; run;
Similarly, the following statements calculate ![]() for the plan n = 20, c = 1 when sampling from a series of lots for which the proportion of nonconforming items is p = 0.18, resulting in a value of 0.1018322793:
for the plan n = 20, c = 1 when sampling from a series of lots for which the proportion of nonconforming items is p = 0.18, resulting in a value of 0.1018322793:
data; prob=probbnml(0.18,20,1); put prob; run;
The measures ASN, AOQ, and ATI are meaningful only for Type B sampling and can be calculated using the PROBBNML function. For reference, the following equations are provided.
Average sample number: Following the notation of Schilling (1982), let ![]() denote the probability of finding c or fewer nonconforming items in a sample of size n. Note that
denote the probability of finding c or fewer nonconforming items in a sample of size n. Note that ![]() is equivalent to PROBBNML
is equivalent to PROBBNML![]() . Then, depending on the mode of inspection, the average sample number can be expressed as shown in the following table:
. Then, depending on the mode of inspection, the average sample number can be expressed as shown in the following table:
|
Mode of Inspection |
ASN |
|---|---|
|
Full |
n |
|
Semicurtailed |
|
|
Fully curtailed |
|
Average outgoing quality can be expressed as
if the nonconforming items found are replaced with conforming items, and as
if the nonconforming items found are not replaced.
Average total inspection can be expressed as