General Criteria :: SAS/QC(R) 13.1 User's Guide

General Criteria

The criteria for an orthogonally confounded $q^ k$ design reduce to requiring that no generalized interactions in a certain set $\mc {M}$ can be confounded with zero. (See the section Structure of General Factorial Designs for a definition of generalized interaction.) This section presents the general definition of $\mc {M}$ . First, define three sets, as follows:

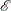
$\mc {E}$: the set of effects that you want to estimate
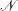
$\mc {N}$: the set of effects that you do not want to estimate but that have unknown nonzero magnitudes (referred to as nonnegligible effects)
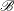
$\mc {B}$: the set of all generalized interactions between block pseudo-factors

Furthermore, for any two sets of effects $\mc {A}$ and $\mc {B}$ , denote by $\mc {A}\times \mc {B}$ the set of all generalized interactions between the effects in $\mc {A}$ and the effects in $\mc {B}$ .

Then the general rules for creating the set of effects $\mc {M}$ that are not to be confounded with zero are as follows:

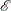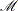Put $\mc {E}$ in $\mc {M}$ . This ensures that all effects in 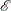$\mc {E}$ are estimable.
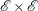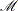Put $\mc {E}\times \mc {E}$ in $\mc {M}$ . This ensures that all pairs of effects in 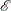$\mc {E}$ are unconfounded with each other.
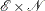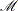Put $\mc {E}\times \mc {N}$ in $\mc {M}$ . This ensures that effects in 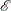$\mc {E}$ are unconfounded with effects in $\mc {N}$ .
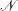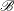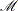Put $\mc {B}$ in $\mc {M}$ . This ensures that all 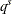$q^ s$ blocks occur in the design.
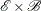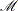Put $\mc {E}\times \mc {B}$ in $\mc {M}$ . This ensures that effects in 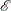$\mc {E}$ are unconfounded with blocks.