New MVPMODEL Procedure
(Experimental)The MVPMODEL procedure provides computational and graphical tools for building a principal components model from multivariate process data in which the measured variables are continuous and correlated. This model then serves as input to the MVPMONITOR procedure.
The MVPMODEL procedure implements principal components analysis (PCA) techniques which evolved in the field of chemometrics for monitoring hundreds or even thousands of correlated process variables; refer to Kourti and MacGregor (1995, 1996) for an introduction. These techniques differ from the classical multivariate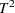 
chart in which Hotelling’s 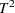statistic is computed as a distance from the multivariate mean scaled by the covariance matrix of the variables; refer to Alt (1985). Instead, principal component methods compute 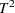based on a small number of principal components that model most of the variation in the data.
The principal components approach offers several advantages over the construction of the classical 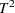chart:
It avoids computational issues that arise when the process variables are collinear and their covariance matrix is nearly singular.
It offers diagnostic tools for interpreting unusual values of
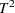. By projecting the data to a low-dimensional subspace, a principal components model more adequately describes the variation in a multivariate process, which is often driven by a small number of underlying factors which are not directly observable.