PROC OPTEX: Optimal Blocking

Optimal Blocking

Building on the work of Harville (1974), Cook and Nachtsheim (1989) give an algorithm for finding D-optimal designs in the presence of fixed block effects. In this case, the design for the original candidate points is called the treatment design. The information matrix for the treatment design has the form 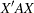$\text{[math]}$ for a certain symmetric, nonnegative-definite matrix 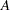$\text{[math]}$ that depends on the blocks. The algorithm is based on two kinds of low-rank changes to the treatment design matrix 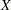$\text{[math]}$ : exchanging a point in the design with a potential treatment point, and interchanging two points in the design. Cook and Nachtsheim (1989) give formulas for computing the resulting change in 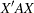$\text{[math]}$ and $\text{[math]}$ . 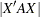These update formulas can be generalized to apply whenever the information matrix for the treatment design has the form 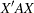$\text{[math]}$ , not just when 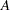$\text{[math]}$ is derived from fixed blocks. This is the basis for the optimal blocking algorithm in the OPTEX procedure.

Notice that you can combine several options to use the OPTEX procedure to evaluate a design with respect to the fixed covariates. Assume the design you want to evaluate is in a data set named Edesign. Then first specify

generate initdesign=Edesign method=sequential;

This makes the data set Edesign the treatment design. Then specify the following BLOCKS statement options:

blocks {block-specification} init=chain iter=0;

The INIT=CHAIN option ensures that the starting ordering for the treatment points is the same as in the Edesign data set, and the ITER=0 specification causes the procedure simply to output the efficiencies for the initial design, without trying to optimize it.