PROC FACTEX: Confounding Rules

Confounding Rules

Confounding rules give the values of factors in terms of the values of the run-indexing factors for a design. (See Types of Factors for a discussion of run-indexing factors.) The FACTEX procedure uses these rules to construct designs. The confounding rules also determine the alias structure of the design. To display the confounding rules for a design, use the CONFOUNDING option in the EXAMINE statement.

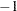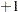For 2-level factors, the rules are displayed in a multiplicative notation that uses the default values of $\text{[math]}$ and $\text{[math]}$ for the factors. For example, the confounding rule

X8 = X1*X2*X3*X4*X5*X6*X7

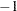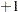means that the level of factor X8 is derived as the product of the levels of factors X1 through X7 for each run in the design. X8 always has a value of $\text{[math]}$ or $\text{[math]}$ since these are the values of X1 through X7. For factors with 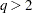$\text{[math]}$ levels, confounding rules are printed in an additive notation, and the arithmetic is performed in the Galois field of size 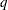$\text{[math]}$ . For example, in a design for 3-level factors, the confounding rule

F = B + (2*C) + D + (2*E)

means that the level of factor F is computed by adding the levels of B and D and two times the levels of C and E, all modulo 3. Note that if 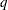$\text{[math]}$ is not a prime number, Galois field arithmetic is not equivalent to arithmetic modulo $\text{[math]}$ .

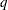Blocks are introduced into designs by using block pseudo-factors. The confounding rule for the 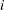$\text{[math]}$ th block pseudo-factor has [Bi] on the left-hand side.

For details about how confounding rules are constructed, see Suitable Confounding Rules.