Default Method

The default estimate for is

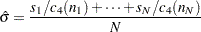where 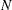is the number of subgroups for which 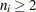, is the sample standard deviation of the 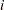th subgroup

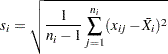and

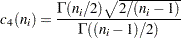Here, 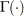denotes the gamma function, and 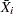denotes the 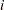th subgroup mean. A subgroup standard deviation is included in the calculation only if 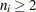. If the observations are normally distributed, then the expected value of is 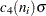. Thus, 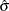is the unweighted average of 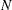unbiased estimates of . This method is described in the American Society for Testing and Materials (1976).

MVLUE Method

If you specify SMETHOD=MVLUE, a minimum variance linear unbiased estimate (MVLUE) is computed for . Refer to Burr (1969, 1976) and Nelson (1989, 1994). This estimate is a weighted average of 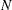unbiased estimates of of the form 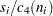, and it is computed as

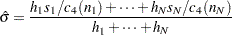where

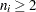A subgroup standard deviation is included in the calculation only if , and 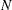is the number of subgroups for which 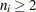. The MVLUE assigns greater weight to estimates of from subgroups with larger sample sizes, and it is intended for situations where the subgroup sample sizes vary. If the subgroup sample sizes are constant, the MVLUE reduces to the default estimate.

MVGRANGE Method

If you specify SMETHOD=MVGRANGE, is estimated using a moving range of subgroup averages. This is appropriate for constructing control charts for means when the 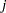th measurement in the 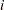th subgroup can be modeled as , where is the between-subgroup variance, 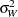is the within-subgroup variance, the 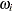are independent with zero mean and unit variance, and the 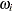are independent of the .

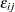The estimate for is

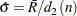where 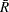is the average of the moving ranges, is the number of consecutive subgroup averages used to compute each moving range, and the unbiasing factor 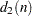is defined so that if the subgroup averages are normally distributed, the expected value of 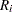is

This method is appropriate for constructing a variation on the three-way control chart that is advocated for this situation by Wheeler (1995). A three-way control chart is useful when sampling, or within-group variation is not the only source of variation, as discussed in Multiple Components of Variation. Wheeler’s three-way control chart comprises a chart of subgroup means, a moving range chart of the subgroup means, and a chart of subgroup ranges. This variation substitutes a chart of subgroup standard deviations for the chart of subgroup ranges. When you specify the SMETHOD=MVGRANGE option, the XSCHART statement produces the appropriate charts of subgroup means and subgroup standard deviations.

RMSDF Method

If you specify SMETHOD=RMSDF, a weighted root-mean-square estimate is computed for .

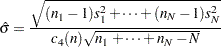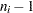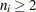The weights are the degrees of freedom . A subgroup standard deviation is included in the calculation only if , and 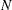is the number of subgroups for which .

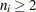If the unknown standard deviation is constant across subgroups, the root-mean-square estimate is more efficient than the minimum variance linear unbiased estimate. However, in process control applications it is generally not assumed that is constant, and if varies across subgroups, the root-mean-square estimate tends to be more inflated than the MVLUE.