Functions: Types of Sampling Plans

Functions

Types of Sampling Plans

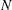In single sampling, a random sample of $\text{[math]}$ items is selected from a lot of size $\text{[math]}$ . If the number $\text{[math]}$ of nonconforming (defective) items found in the sample is less than or equal to an acceptance number $\text{[math]}$ , the lot is accepted. Otherwise, the lot is rejected.

In double sampling, a sample of size $\text{[math]}$ is drawn from the lot, and the number $\text{[math]}$ of nonconforming items is counted. If $\text{[math]}$ is less than or equal to an acceptance number $\text{[math]}$ , the lot is accepted, and if $\text{[math]}$ is greater than or equal to a rejection number $\text{[math]}$ , the lot is rejected. Otherwise, if $\text{[math]}$ , a second sample of size $\text{[math]}$ is taken, and the number of nonconforming items $\text{[math]}$ is counted. Then if $\text{[math]}$ is less than or equal to an acceptance number $\text{[math]}$ , the lot is accepted, and if $\text{[math]}$ is greater than or equal to a rejection number $\text{[math]}$ , the lot is rejected. This notation follows that of Schilling (1982). Note that some authors, including Montgomery (1996), define the first rejection number using a strict inequality.

In Type A sampling, the sample is intended to represent a single, finite-sized lot, and the characteristics of the sampling plan depend on 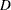$\text{[math]}$ , the number of nonconforming items in the lot, as well as 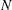$\text{[math]}$ , $\text{[math]}$ , and $\text{[math]}$ .

In Type B sampling, the sample is intended to represent a series of lots (or the lot size is effectively infinite), and the characteristics of the sampling plan depend on 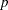$\text{[math]}$ , the proportion of nonconforming items produced by the process, as well as $\text{[math]}$ and $\text{[math]}$ .

A hypergeometric model is appropriate for Type A sampling, and a binomial model is appropriate for Type B sampling.

Top of Page