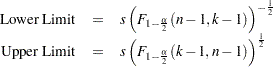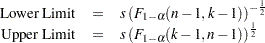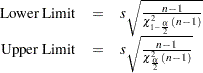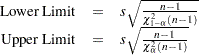| The CAPABILITY Procedure |
Methods for Computing Statistical Intervals
The formulas for statistical intervals given in this section use the following notation:
Notation |
Definition |
|---|---|
|
number of nonmissing values for a variable |
|
mean of variable |
|
standard deviation of variable |
|
100 |
|
100 |
|
100 |
parameter |
|
|
100 |
the numerator and |
|
|
100 |
The values of the variable are assumed to be independent and normally distributed. The intervals are computed using the degrees of freedom as the divisor for the standard deviation  . This divisor corresponds to the default of VARDEF=DF in the PROC CAPABILITY statement. If you specify another value for the VARDEF= option, intervals are not computed.
. This divisor corresponds to the default of VARDEF=DF in the PROC CAPABILITY statement. If you specify another value for the VARDEF= option, intervals are not computed.
You select the intervals to be computed with the METHODS= option. The next six sections give computational details for each of the METHODS= options.
METHODS=1
This requests an approximate simultaneous prediction interval for  future observations. Two-sided intervals are computed using the conservative approximations
future observations. Two-sided intervals are computed using the conservative approximations
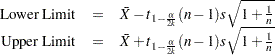
One-sided limits are computed using the conservative approximation
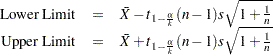
Hahn (1970c) states that these approximations are satisfactory except for combinations of small  , large
, large  , and large
, and large  . Refer also to Hahn (1969, 1970a) and Hahn and Meeker (1991).
. Refer also to Hahn (1969, 1970a) and Hahn and Meeker (1991).
METHODS=2
This requests a prediction interval for the mean of  future observations. Two-sided intervals are computed as
future observations. Two-sided intervals are computed as
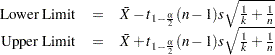
One-sided limits are computed as
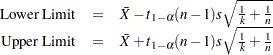
METHODS=3
This requests an approximate statistical tolerance interval that contains at least proportion 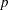 of the population. Two-sided intervals are approximated by
of the population. Two-sided intervals are approximated by
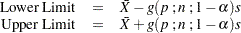
where 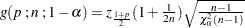 .
.
Exact one-sided limits are computed as
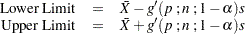
where 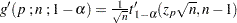 .
.
In some cases (for example, if 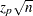 is large),
is large), 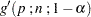 is approximated by
is approximated by
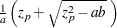
where 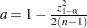 and
and 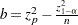 .
.
Hahn (1970b) states that this approximation is "poor for very small  , especially for large
, especially for large 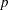 and large
and large  , and is not advised for
, and is not advised for 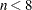 ." Refer also to Hahn and Meeker (1991).
." Refer also to Hahn and Meeker (1991).
METHODS=4
This requests a confidence interval for the population mean. Two-sided intervals are computed as
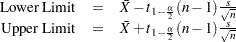
One-sided limits are computed as
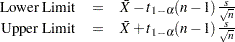
Copyright © SAS Institute, Inc. All Rights Reserved.

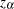
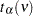
 distribution with
distribution with  degrees of freedom
degrees of freedom 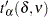
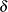 and
and 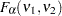
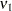 degrees of freedom in
degrees of freedom in 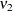 degrees of freedom in the denominator
degrees of freedom in the denominator 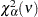
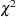 distribution with
distribution with