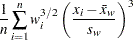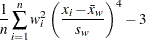| The UNIVARIATE Procedure |
| Descriptive Statistics |
This section provides computational details for the descriptive statistics that are computed with the PROC UNIVARIATE statement. These statistics can also be saved in the OUT= data set by specifying the keywords listed in Table 4.43 in the OUTPUT statement.
Standard algorithms (Fisher; 1973) are used to compute the moment statistics. The computational methods used by the UNIVARIATE procedure are consistent with those used by other SAS procedures for calculating descriptive statistics.
The following sections give specific details on a number of statistics calculated by the UNIVARIATE procedure.
Mean
The sample mean is calculated as
 |
where  is the number of nonmissing values for a variable,
is the number of nonmissing values for a variable, 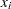 is the
is the 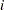 th value of the variable, and
th value of the variable, and 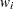 is the weight associated with the
is the weight associated with the 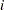 th value of the variable. If there is no WEIGHT variable, the formula reduces to
th value of the variable. If there is no WEIGHT variable, the formula reduces to
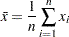 |
Sum
The sum is calculated as  , where
, where  is the number of nonmissing values for a variable,
is the number of nonmissing values for a variable, 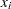 is the
is the 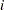 th value of the variable, and
th value of the variable, and 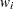 is the weight associated with the
is the weight associated with the 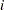 th value of the variable. If there is no WEIGHT variable, the formula reduces to
th value of the variable. If there is no WEIGHT variable, the formula reduces to  .
.
Sum of the Weights
The sum of the weights is calculated as 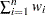 , where
, where  is the number of nonmissing values for a variable and
is the number of nonmissing values for a variable and 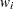 is the weight associated with the
is the weight associated with the 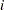 th value of the variable. If there is no WEIGHT variable, the sum of the weights is
th value of the variable. If there is no WEIGHT variable, the sum of the weights is  .
.
Variance
The variance is calculated as
 |
where  is the number of nonmissing values for a variable,
is the number of nonmissing values for a variable, 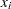 is the
is the 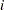 th value of the variable,
th value of the variable, 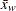 is the weighted mean,
is the weighted mean, 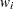 is the weight associated with the
is the weight associated with the 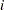 th value of the variable, and
th value of the variable, and 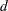 is the divisor controlled by the VARDEF= option in the PROC UNIVARIATE statement:
is the divisor controlled by the VARDEF= option in the PROC UNIVARIATE statement:
 |
If there is no WEIGHT variable, the formula reduces to
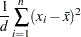 |
Standard Deviation
The standard deviation is calculated as
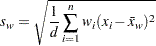 |
where  is the number of nonmissing values for a variable,
is the number of nonmissing values for a variable, 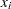 is the
is the 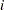 th value of the variable,
th value of the variable, 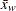 is the weighted mean,
is the weighted mean, 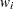 is the weight associated with the
is the weight associated with the 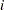 th value of the variable, and
th value of the variable, and 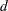 is the divisor controlled by the VARDEF= option in the PROC UNIVARIATE statement. If there is no WEIGHT variable, the formula reduces to
is the divisor controlled by the VARDEF= option in the PROC UNIVARIATE statement. If there is no WEIGHT variable, the formula reduces to
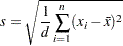 |
Skewness
The sample skewness, which measures the tendency of the deviations to be larger in one direction than in the other, is calculated as follows depending on the VARDEF= option:
VARDEF |
Formula |
|---|---|
DF (default) |
|
N |
|
WDF |
missing |
WEIGHT | WGT |
missing |
where  is the number of nonmissing values for a variable,
is the number of nonmissing values for a variable, 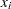 is the
is the 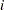 th value of the variable,
th value of the variable, 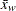 is the sample average,
is the sample average,  is the sample standard deviation, and
is the sample standard deviation, and 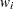 is the weight associated with the
is the weight associated with the 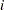 th value of the variable. If VARDEF=DF, then
th value of the variable. If VARDEF=DF, then  must be greater than 2. If there is no WEIGHT variable, then
must be greater than 2. If there is no WEIGHT variable, then 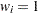 for all
for all  .
.
The sample skewness can be positive or negative; it measures the asymmetry of the data distribution and estimates the theoretical skewness 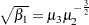 , where
, where 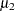 and
and 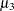 are the second and third central moments. Observations that are normally distributed should have a skewness near zero.
are the second and third central moments. Observations that are normally distributed should have a skewness near zero.
Kurtosis
The sample kurtosis, which measures the heaviness of tails, is calculated as follows depending on the VARDEF= option:
VARDEF |
Formula |
|---|---|
DF (default) |
|
N |
|
WDF |
missing |
WEIGHT | WGT |
missing |
where  is the number of nonmissing values for a variable,
is the number of nonmissing values for a variable, 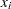 is the
is the 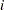 th value of the variable,
th value of the variable, 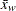 is the sample average,
is the sample average,  is the sample standard deviation, and
is the sample standard deviation, and 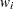 is the weight associated with the
is the weight associated with the 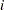 th value of the variable. If VARDEF=DF, then
th value of the variable. If VARDEF=DF, then  must be greater than 3. If there is no WEIGHT variable, then
must be greater than 3. If there is no WEIGHT variable, then 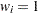 for all
for all  .
.
The sample kurtosis measures the heaviness of the tails of the data distribution. It estimates the adjusted theoretical kurtosis denoted as 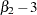 , where
, where 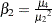 , and
, and  is the fourth central moment. Observations that are normally distributed should have a kurtosis near zero.
is the fourth central moment. Observations that are normally distributed should have a kurtosis near zero.
Coefficient of Variation (CV)
The coefficient of variation is calculated as
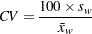 |
Copyright © SAS Institute, Inc. All Rights Reserved.