PROC DTREE interprets a decision problem represented in SAS data sets, finds the optimal decisions, and plots on a line printer or a graphics device the decision tree showing the optimal decisions. A decision tree contains two types of nodes: decision nodes and chance nodes. A decision node represents a stage in the problem where a decision is to be made that could lead you along different paths through the tree. A chance node represents a stage in the problem where some uncertain factors result in one of several possible outcomes, once again leading you to different branches of the tree, with associated probabilities.

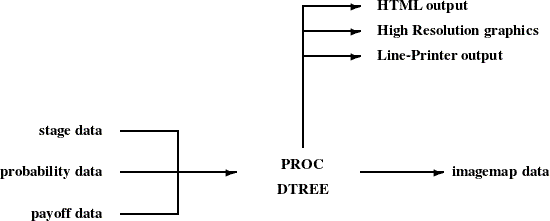
The structure of a decision model is given in the STAGEIN= data set. This data set, described in detail in Chapter 7: The DTREE Procedure, specifies the name, type, and attributes of all outcomes for each stage in your model. This is the only data set that is required to produce a diagrammatic representation of your decision problem. To evaluate and analyze your decision model, you need to specify the PROBIN= and PAYOFFS= data sets. The PROBIN= data set specifies the conditional probabilities for every event in your model. The PAYOFFS= data set specifies the value of each possible scenario (sequence of outcomes). The objective is to use the information summarized in these data sets to determine the optimal decision based on some measure of performance. One common objective is to maximize the expected value of the return. Figure 3.7 illustrates the data flow for PROC DTREE.

You can use PROC DTREE to display, evaluate, and summarize your decision problem. The procedure can be used to plot the decision tree in line-printer or graphics mode. The optimal decisions are highlighted on the output. Further, a summary table can be displayed listing all paths through the decision tree along with the cumulative reward and the evaluating values of all alternatives for that path. The summary table indicates the optimal evaluating value for each path with an asterisk. The procedure can also perform sensitivity analysis and what-if analysis. A simple decision problem is described in Example 3.9.