Introduction to Optimization

Model generation and maintenance are often difficult and expensive aspects of applying mathematical programming techniques. The richly expressive syntax and features of PROC OPTMODEL, in addition to the flexible data input and output capabilities, simplify this task considerably. Although PROC OPTMODEL offers almost unlimited latitude in how a particular optimization problem is formulated, the most effective use of OPTMODEL is achieved when the model is abstracted away from the data. This aspect makes PROC OPTMODEL somewhat unusual among SAS procedures and is important enough to illustrate with a simple example.

A small product-mix problem serves as a starting point for a discussion of two different ways of modeling with PROC OPTMODEL.

A candy manufacturer makes two products: chocolate and toffee. What combination of chocolate and toffee should be produced in a day in order to maximize the company’s profit? Chocolate contributes $0.25 per pound to profit, and toffee contributes $0.75 per pound. The decision variables are chocolate and toffee.

Four processes are used to manufacture the candy:

During the day, there are 7.5 hours (27,000 seconds) available for each process.

Firm time standards have been established for each process. For Process 1, mixing and cooking take 15 seconds for each pound of chocolate, and 40 seconds for each pound of toffee. Process 2 takes 56.25 seconds per pound of toffee. For Process 3, each pound of chocolate requires 18.75 seconds of processing. In packaging, a pound of chocolate can be wrapped in 12 seconds, whereas a pound of toffee requires 50 seconds. These data are summarized as follows:

                      Available       Required per Pound
                        Time         chocolate     toffee
     Process            (sec)          (sec)         (sec)
   1 Cooking            27,000           15          40
   2 Color/Flavor       27,000                      56.25
   3 Condiments         27,000          18.75
   4 Packaging          27,000           12          50

The objective is to maximize the company’s total profit, which is represented as

 Maximize: 0.25(chocolate) + 0.75(toffee)

The production of the candy is limited by the time available for each process. The limits placed on production by Process 1 are expressed by the following inequality:

 Process 1: 15(chocolate) + 40(toffee)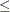 27,000

Process 1 can handle any combination of chocolate and toffee that satisfies this inequality.

The limits on production by other processes generate constraints described by the following inequalities:

 Process 2: 56.25(toffee) 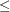27,000

 Process 3: 18.75(chocolate) 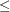27,000

 Process 4: 12(chocolate) + 50(toffee) 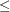27,000

This linear program illustrates an example of a product mix problem. The mix of products that maximizes the objective without violating the constraints is the solution.

First, the following statements demonstrate a way of representing the optimization model in PROC OPTMODEL that is almost a verbatim translation of the mathematical model:

proc optmodel;
   /* declare variables */
   var choco >= 0, toffee >= 0;

   /* maximize objective function (profit) */
   maximize profit = 0.25*choco + 0.75*toffee;

   /* subject to constraints */
   con process1:    15*choco +    40*toffee <= 27000;
   con process2:               56.25*toffee <= 27000;
   con process3: 18.75*choco                <= 27000;
   con process4:    12*choco +    50*toffee <= 27000;

   /* solve LP using primal simplex solver */
   solve with lp / solver = primal_spx;

   /* display solution */
   print choco toffee;
quit;

The optimal objective value and the optimal solution are displayed in Figure 3.1:

You can observe from the preceding example that PROC OPTMODEL provides an easy and very direct way of modeling and solving mathematical programming models. Although this way of modeling, where the data are intertwined heavily with model elements, is correct, has significant practical limitations. The model is not easy to explain, it is hard to generalize, and clearly this approach does not scale to large problems of the same type. To overcome these issues, you need to separate the data from the essential algebraic structure of the model. Along those lines, you can make the reasonable assumption that you have the following two data sets (one for the products and one for processes that capture the parameters and data elements of this product mix problem):

data Products;
   length Name $10.;
   input Name $ Profit;
datalines;
Chocolate  0.25
Toffee     0.75
;

data Processes;
   length Name $15.;
   input Name $ Available_time Chocolate Toffee;
datalines;
Cooking            27000           15          40
Color/Flavor       27000            0          56.25
Condiments         27000          18.75         0
Packaging          27000           12          50
;

The following alternative model in PROC OPTMODEL can solve the same problem by taking these data sets as input:

proc optmodel;
   /* declare sets and data indexed by sets */
   set <string> Products;
   set <string> Processes;
   num Profit{Products};
   num AvailableTime{Processes};
   num RequiredTime{Products,Processes};
   /* declare the variable */
   var Amount{Products};
   /* maximize objective function (profit) */
   maximize TotalProfit = sum{p in Products} Profit[p]*Amount[p];
   /* subject to constraints */
   con Availability{r in Processes}:
      sum{p in Products} RequiredTime[p,r]*Amount[p] <= AvailableTime[r];
   /* abstract algebraic model that captures the structure of the */
   /*    optimization problem has been defined without referring  */
   /*    to a single data constant                                */
   /* populate model by reading in the specific data instance */
   read data Products into Products=[name] Profit;
   read data Processes into Processes=[name] AvailableTime=Available_time
      {p in Products} <RequiredTime[p,name]= col(p)>;
   /* solve LP using primal simplex solver */
   solve with lp / solver = primal_spx;
   /* display solution */
   print Amount;
quit;

The details of the syntax and elements of the PROC OPTMODEL language are discussed in Chapter 5: The OPTMODEL Procedure. The key observation here is that the preceding version of the PROC OPTMODEL statements capture the essence of the optimization model concisely, but completely, and the model can be explained, modified, and maintained easily. It also achieves total separation of the data from the model in that the same PROC OPTMODEL statements can be applied to any other specific problem of this type (and of any size) by simply changing the data sets appropriately and rerunning the same PROC OPTMODEL statements. Also, because of PROC OPTMODEL’s ability to read data very flexibly and from any number of data sets, the problem data can be in its most natural form, making the model easier to explain and understand.