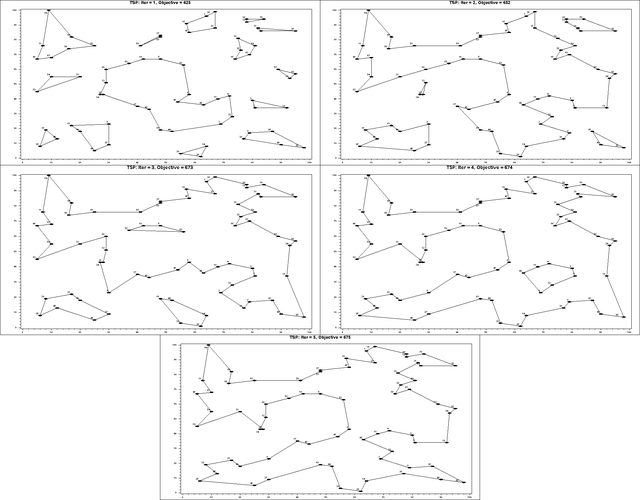
This example demonstrates the use of the SUBMIT statement to execute a block of SAS statements from within a PROC OPTMODEL session. In this case, the SUBMIT block calls the GPLOT procedure to display intermediate results during the solution of an instance of the traveling salesman problem (TSP). The problem is described in Example 7.4. See the “Examples” section in Chapter 2: The OPTNET Procedure in SAS/OR 12.3 User's Guide: Network Optimization Algorithms . for an example of how to use PROC OPTNET to solve the TSP.

The following DATA step converts a TSPLIB instance of type EUC_2D into a SAS data set that contains the coordinates of the vertices:

/* convert the TSPLIB instance into a data set */
data tspData(drop=H);
   infile "&tsplib";
   input H $1. @;
   if H not in ('N','T','C','D','E');
   input @1 var1-var3;
run;

The following macro generates plots of the solution and objective value:

%macro plotTSP;
   /* create Annotate data set to draw subtours */
   data anno(drop=xi yi xj yj);
      %SYSTEM(2, 2, 2);
      set solData(keep=xi yi xj yj);
      %LINE(xi, yi, xj, yj, *, 1, 1);
   run;

   title1 h=2 "TSP: Iter = &i, Objective = &&obj&i";
   title2;

%* sas;
   %put iteration i: &i.;
%* tex;
   proc gplot data=tspData anno=anno;
%* sas;
   proc gplot data=tspData anno=anno gout=tspg;
      axis1 label=none;
      symbol1 value=dot interpol=none
      pointlabel=("#var1" nodropcollisions height=1) cv=black;
      plot var3*var2 / haxis=axis1 vaxis=axis1;
   run;
   quit;
%mend plotTSP;

%annomac;

The following PROC OPTMODEL statements solve the TSP by using the subtour formulation and iteratively adding subtour constraints. The SUBMIT statement calls the %plotTSP macro to plot the solution and objective value at each stage.

/* iterative solution using the subtour formulation */
proc optmodel;
   set VERTICES;
   set EDGES = {i in VERTICES, j in VERTICES: i > j};
   num xc {VERTICES};
   num yc {VERTICES};

   num numsubtour init 0;
   set SUBTOUR {1..numsubtour};

   /* read in the instance and customer coordinates (xc, yc) */
   read data tspData into VERTICES=[var1] xc=var2 yc=var3;

   /* the cost is the euclidean distance rounded to the nearest integer */
   num c {<i,j> in EDGES}
      init floor( sqrt( ((xc[i]-xc[j])**2 + (yc[i]-yc[j])**2)) + 0.5);

   var x {EDGES} binary;

   /* minimize the total cost */
   min obj =
       sum {<i,j> in EDGES} c[i,j] * x[i,j];

   /* each vertex has exactly one in-edge and one out-edge */
   con two_match {i in VERTICES}:
      sum {j in VERTICES: i > j} x[i,j]
      + sum {j in VERTICES: i < j} x[j,i] = 2;

   /* no subtours (these constraints are generated dynamically) */
   con subtour_elim {s in 1..numsubtour}:
      sum {<i,j> in EDGES: (i in SUBTOUR[s] and j not in SUBTOUR[s])
         or (i not in SUBTOUR[s] and j in SUBTOUR[s])} x[i,j] >= 2;

   /* this starts the algorithm to find violated subtours */
   set <num,num> EDGES1;
   set INITVERTICES = setof{<i,j> in EDGES1} i;
   set VERTICES1;
   set NEIGHBORS;
   set <num,num> CLOSURE;
   num component {INITVERTICES};
   num numcomp  init 2;
   num iter     init 1;
   call symput('i',trim(left(put(round(iter),best.))));
   num numiters init 1;

   /* initial solve with just matching constraints */
   solve;
   call symput(compress('obj'||put(iter,best.)),
              trim(left(put(round(obj),best.))));

   /* create a data set for use by PROC GPLOT */
   create data solData from
      [i j]={<i,j> in EDGES: x[i,j].sol > 0.5}
      xi=xc[i] yi=yc[i] xj=xc[j] yj=yc[j];
   submit;
      %plotTSP;
   endsubmit;

   /* while the solution is disconnected, continue */
   do while (numcomp > 1);
      iter = iter + 1;
      call symput('i',trim(left(put(round(iter),best.))));

      /* find connected components of support graph   */
      EDGES1 = {<i,j> in EDGES: round(x[i,j].sol) = 1};
      EDGES1 = EDGES1 union {setof {<i,j> in EDGES1} <j,i>};
      VERTICES1 = INITVERTICES;
      CLOSURE = EDGES1;

      for {i in INITVERTICES} component[i] = 0;
      for {i in VERTICES1} do;
         NEIGHBORS = slice(<i,*>,CLOSURE);
         CLOSURE = CLOSURE union (NEIGHBORS cross NEIGHBORS);
      end;

      numcomp = 0;
      do while (card(VERTICES1) > 0);
         numcomp = numcomp + 1;
         for {i in VERTICES1} do;
            NEIGHBORS = slice(<i,*>,CLOSURE);
            for {j in NEIGHBORS} component[j] = numcomp;
            VERTICES1 = VERTICES1 diff NEIGHBORS;
            leave;
         end;
      end;

      if numcomp = 1 then leave;

      numiters = iter;
      numsubtour = numsubtour + numcomp;
      for {comp in 1..numcomp} do;
         SUBTOUR[numsubtour-numcomp+comp]
           = {i in VERTICES: component[i] = comp};
      end;

      solve;
      call symput(compress('obj'||put(iter,best.)),
                 trim(left(put(round(obj),best.))));

      /* create a data set for use by PROC GPLOT */
      create data solData from
         [i j]={<i,j> in EDGES: x[i,j].sol > 0.5}
         xi=xc[i] yi=yc[i] xj=xc[j] yj=yc[j];

      call symput('numiters',put(numiters,best.));
      submit;
         %plotTSP;
      endsubmit;
   end;
quit;

The plot in Output 5.6.1 shows the solution and objective value at each stage. Each stage restricts some subset of subtours. When you reach the final stage, you have a valid tour.