| The Mixed Integer Linear Programming Solver |
Overview: MILP Solver
The OPTMODEL procedure provides a framework for specifying and solving mixed integer linear programs (MILPs). A standard mixed integer linear program has the following formulation:
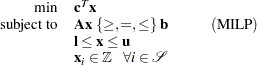 |
where
|
|
|
is the vector of structural variables |
|
|
|
is the matrix of technological coefficients |
|
|
|
is the vector of objective function coefficients |
|
|
|
is the vector of constraints right-hand sides (RHS) |
|
|
|
is the vector of lower bounds on variables |
|
|
|
is the vector of upper bounds on variables |
|
is a nonempty subset of the set |
The MILP solver, available in the OPTMODEL procedure, implements an LP-based branch-and-bound algorithm. This divide-and-conquer approach attempts to solve the original problem by solving linear programming relaxations of a sequence of smaller subproblems. The MILP solver also implements advanced techniques such as presolving, generating cutting planes, and applying primal heuristics to improve the efficiency of the overall algorithm.
The MILP solver provides various control options and solution strategies. In particular, you can enable, disable, or set levels for the advanced techniques previously mentioned. It is also possible to input an incumbent solution; see the section Warm Start Option for details.
Copyright © SAS Institute, Inc. All Rights Reserved.



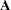
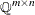


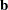


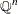

 of indices
of indices