| The LP Procedure |
| Sensitivity Analysis |
Sensitivity analysis is a technique for examining the effects of changes in model parameters on the optimal solution. The analysis enables you to examine the size of a perturbation to the right-hand-side or objective vector by an arbitrary change vector for which the basis of the current optimal solution remains optimal.
Note:When sensitivity analysis is performed on integer-constrained problems, the integer variables are fixed at the value they obtained in the integer optimal solution. Therefore, care must be used when interpreting the results of such analyses. Care must also be taken when preprocessing is enabled, because preprocessing usually alters the original formulation.
Right-Hand-Side Sensitivity Analysis
Consider the problem 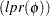 :
:
 |
where  is a right-hand-side change vector.
is a right-hand-side change vector.
Let 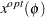 denote an optimal basic feasible solution to
denote an optimal basic feasible solution to 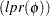 . PROC LP can be used to examine the effects of changes in
. PROC LP can be used to examine the effects of changes in 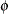 on the solution
on the solution  of problem
of problem 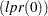 . For the basic solution
. For the basic solution  , let
, let 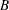 be the matrix composed of the basic columns of
be the matrix composed of the basic columns of  and let
and let 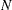 be the matrix composed of the nonbasic columns of
be the matrix composed of the nonbasic columns of  . For the basis matrix
. For the basis matrix 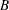 , the basic components of
, the basic components of  , written as
, written as  , can be expressed as
, can be expressed as
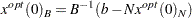 |
Furthermore, because  is feasible,
is feasible,
 |
where 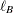 is a column vector of the lower bounds on the structural basic variables, and
is a column vector of the lower bounds on the structural basic variables, and 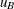 is a column vector of the upper bounds on the structural basic variables. For each right-hand-side change vector
is a column vector of the upper bounds on the structural basic variables. For each right-hand-side change vector  identified in the RHSSEN statement, PROC LP finds an interval
identified in the RHSSEN statement, PROC LP finds an interval 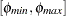 such that
such that
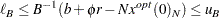 |
for 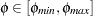 . Furthermore, because changes in the right-hand side do not affect the reduced costs, for
. Furthermore, because changes in the right-hand side do not affect the reduced costs, for 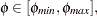
 |
is optimal in 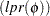 .
.
For 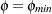 and
and  , PROC LP reports the following:
, PROC LP reports the following:
the names of the leaving variables
the value of the optimal objective in the modified problems
the RHS values in the modified problems
the solution status, reduced costs and activities in the modified problems
The leaving variable identifies the basic variable 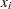 that first reaches either the lower bound
that first reaches either the lower bound 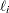 or the upper bound
or the upper bound  as
as 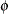 reaches
reaches 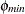 or
or  . This is the basic variable that would leave the basis to maintain primal feasibility. Multiple RHSSEN variables can appear in a problem data set.
. This is the basic variable that would leave the basis to maintain primal feasibility. Multiple RHSSEN variables can appear in a problem data set.
Price Sensitivity Analysis
Consider the problem 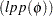 :
:
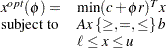 |
where  is a price change vector.
is a price change vector.
Let 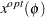 denote an optimal basic feasible solution to
denote an optimal basic feasible solution to  . PROC LP can be used to examine the effects of changes in
. PROC LP can be used to examine the effects of changes in 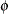 on the solution
on the solution  of problem
of problem 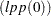 . For the basic solution
. For the basic solution  , let
, let 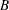 be the matrix composed of the basic columns of
be the matrix composed of the basic columns of  and let
and let 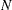 be the matrix composed of the nonbasic columns of
be the matrix composed of the nonbasic columns of  . For basis matrix
. For basis matrix 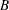 , the reduced cost associated with the
, the reduced cost associated with the  th variable can be written as
th variable can be written as
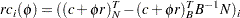 |
where 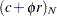 and
and  is a partition of the vector of price coefficients into nonbasic and basic components. Because
is a partition of the vector of price coefficients into nonbasic and basic components. Because  is optimal in
is optimal in 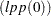 , the reduced costs satisfy
, the reduced costs satisfy
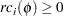 |
if the nonbasic variable in column  is at its lower bound, and
is at its lower bound, and
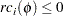 |
if the nonbasic variable in column  is at its upper bound.
is at its upper bound.
For each price coefficient change vector  identified with the keyword PRICESEN in the TYPE variable, PROC LP finds an interval
identified with the keyword PRICESEN in the TYPE variable, PROC LP finds an interval 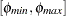 such that for
such that for 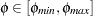 ,
,
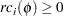 |
if the nonbasic variable in column  is at its lower bound, and
is at its lower bound, and
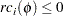 |
if the nonbasic variable in column  is at its upper bound. Because changes in the price coefficients do not affect feasibility, for
is at its upper bound. Because changes in the price coefficients do not affect feasibility, for 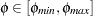 ,
, 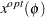 is optimal in
is optimal in 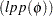 . For
. For 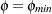 and
and  , PROC LP reports the following:
, PROC LP reports the following:
the names of entering variables
the value of the optimal objective in the modified problems
the price coefficients in the modified problems
the solution status, reduced costs, and activities in the modified problems
The entering variable identifies the variable whose reduced cost first goes to zero as 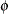 reaches
reaches 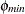 or
or  . This is the nonbasic variable that would enter the basis to maintain optimality (dual feasibility). Multiple PRICESEN variables may appear in a problem data set.
. This is the nonbasic variable that would enter the basis to maintain optimality (dual feasibility). Multiple PRICESEN variables may appear in a problem data set.
Copyright © SAS Institute, Inc. All Rights Reserved.