Primal-dual interior point methods can be classified into two categories: feasible and infeasible. The first category requires the starting point in addition to all subsequent iterations of the algorithm to strictly satisfy all the inequality constraints. The second category relaxes those requirements and allows the iterations to violate some or all of the inequality constraints during the course of the minimization procedure. Currently, the IPNLP solver implements an infeasible algorithm, so this section concentrates on that type of algorithm.

To make the notation less cluttered and the fundamentals of interior point methods easier to understand, consider without loss of generality the following simpler NLP problem:

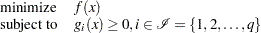Note that the equality and bound constraints have been omitted from the preceding problem. Initially, slack variables are added to the inequality constraints, giving rise to the problem

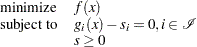where represents the vector of the slack variables, which are required to be nonnegative. Next, all the nonnegativity constraints on the slack variables are eliminated by being incorporated into the objective function, by means of a logarithmic function. This gives rise to the equality-constrained NLP problem

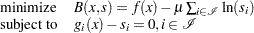where 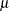is a positive parameter. The preceding problem is often called the barrier problem. The nonnegativity constraints on the slack variables are implicitly enforced by the logarithmic functions, since the logarithmic function prohibits from taking zero or negative values.

Depending on the size of the parameter 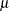, a local minimum of the barrier problem provides an approximation to the local minimum of the original NLP problem. The smaller the size of 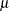, the better the approximation becomes. Infeasible primal-dual interior point algorithms repeatedly solve the barrier problem for different values of 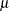that progressively go to zero, in order to get as close as possible to a local minimum of the original NLP problem.

To solve the barrier problem, first define its Lagrangian function

Then, define its first-order optimality conditions

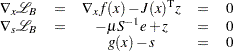where 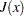represents the Jacobian matrix of the vector function , 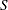represents the diagonal matrix whose elements are the elements of the vector (that is, ), and represents a vector of all ones. Multiplying the second equation by 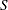produces the following equivalent nonlinear system:

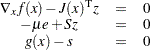Note that if 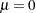, the preceding conditions represent the optimality conditions of the original optimization problem, after adding slack variables. One of the main aims of the algorithm is to gradually reduce the value of 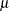to zero, so that it converges to a local optimum of the original NLP problem. The rate by which 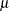approaches zero affects the overall efficiency of the algorithm.

At an iteration 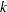, the infeasible primal-dual interior point algorithm approximately solves the preceding system by using Newton’s method. The Newton system is

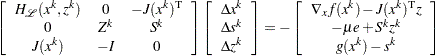where 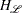is the Hessian matrix of the Lagrangian function of the original NLP problem; that is,

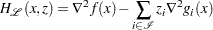The solution of the Newton system provides a direction to move from the current iteration 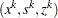to the next,

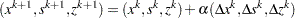where is the step length along the Newton direction. The step length is determined through a line-search procedure that ensures sufficient decrease of a merit function based on the augmented Lagrangian function of the barrier problem. The role of the merit function and the line-search procedure is to ensure that the objective and the infeasibility reduce sufficiently at every iteration and that the iterations approach a local minimum of the original NLP problem.