Overview: IPNLP Solver

The interior point nonlinear programming (IPNLP) solver component of the OPTMODEL procedure can solve nonlinear programming (NLP) problems that contain both nonlinear equality and inequality constraints. The general NLP problem can be defined as

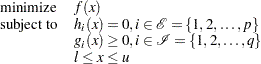where 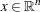represents the vector of the decision variables; 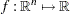represents the objective function; 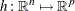represents the vector of equality constraints—that is, 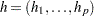; 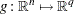represents the vector of inequality constraints—that is, 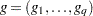; and 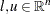represent the vectors of the lower and upper bounds, respectively, on the decision variables.

It is assumed that the functions 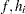, and 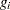are twice continuously differentiable. Any point that satisfies the constraints of the NLP problem is called a feasible point, and the set of all those points forms the feasible region of the NLP problem—that is, .

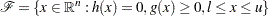The NLP problem can have a unique minimum or many different minima, depending on the type of functions involved in it. If the objective function is convex, the equality constraint functions are linear, and the inequality constraint functions are concave, then the NLP problem is called a convex program and has a unique minimum. All other types of NLP problems are called nonconvex and can contain more than one minimum, usually called local minima. The solution that achieves the least of all the local minima is called the global minimum or the global solution of the NLP problem. The IPNLP solver can find the unique solution of convex programs in addition to a local minimum of a general NLP problem.

The IPNLP solver implements the following two primal-dual interior point methods:

• an iterative trust-region algorithm

• a quasi-Newton line-search algorithm

The first method is recommended for large-scale optimization problems, which might contain many thousands of variables or constraints or both. It uses exact first and second derivatives to calculate the search direction. The memory requirements of the algorithm are reduced dramatically because only nonzero elements of matrices are stored. Convergence of the algorithm is achieved by using a trust-region framework that guides the iterations of the algorithm towards the solution of the optimization problem.

The second method uses a quasi-Newton approach to solve the optimization problem. As such, it needs to calculate only the gradients of the objective and constraints and from this it approximates the second derivatives. It also uses a line-search procedure and a merit function to ensure convergence of the iterations to a local minimum. This method is more appropriate for problems where the second derivatives of the objective or constraints or both require a lot of computational effort.

Both methods incorporate many powerful features that are obtained from recent research in the field of primal-dual interior point algorithms (Akrotirianakis and Rustem; 2005; Armand, Gilbert, and Jan-Jégou; 2002; Vanderbei and Shanno; 1999; Wächter and Biegler; 2006; Yamashita; 1998; Forsgren and Gill; 1998; Erway, Gill, and Griffin; 2007). The term primal-dual means that the algorithm iteratively generates better approximations of the decision variables (usually called primal variables) in addition to the dual variables (also referred to as Lagrange multipliers). At every iteration, the algorithm uses a modified Newton’s method to solve a system of nonlinear equations. The solution of that system provides the direction and the steps along which the next approximation of the local minimum is searched. The quasi-Newton algorithm ensures that the primal iterations are always strictly within their bounds—that is, 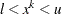, for every iteration 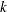. However, the iterative approach relaxes this condition, and intermediate iterations might be infeasible.