At each iteration 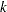, the conjugate gradient (CONGRA), Newton-type (NEWTYP) and quasi-Newton (QUANEW) optimization techniques use iterative line-search algorithms. These algorithms try to optimize a quadratic or cubic approximation of some merit function along the search direction 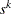by computing an approximately optimal step length 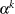that is used as follows:

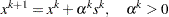A line-search algorithm is an iterative process that optimizes a nonlinear function of one variable within each iteration 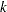of the main optimization algorithm, which itself tries to optimize a quadratic approximation of the nonlinear objective function 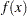. Since the outside iteration process is based only on the approximation of the objective function, the inside iteration of the line-search algorithm does not have to be perfect. Usually the appropriate choice of is one that significantly reduces (in the case of minimization) the objective function value. Criteria often used for termination of line-search algorithms are the Goldstein conditions; see Fletcher (1987).

The line-search method in the NLPC solver is implemented as described in Fletcher (1987).