Overview: NLPC Nonlinear Optimization Solver

In nonlinear optimization, we try to minimize or maximize an objective function that can be subject to a set of constraints. The objective function is typically nonlinear in terms of the decision variables. If the problem is constrained, it can be subject to bound, linear, or nonlinear constraints. In general, we can classify nonlinear optimization (minimization or maximization) problems into the following four categories:

• unconstrained

• bound constrained

• linearly constrained

• nonlinearly constrained

Since a maximization problem is equivalent to minimizing the negative of the same objective function, the general form of nonlinear optimization problems can, without loss of generality, be mathematically described as follows:

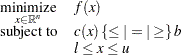where 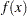: 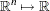is the nonlinear objective function; 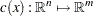are the functions of general nonlinear equality and inequality constraints, also referred to as the body of constraints; 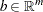are the constant terms of the constraints, also referred to as the right-hand side (RHS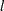); and and are lower and upper bounds on the decision variable . If 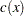are all linear in , the nonlinear optimization problem becomes a linearly constrained problem, which can be expressed as follows:

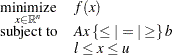where 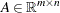. If 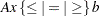is not present, we have a bound constrained problem. If it is also true that 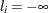and 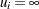for all 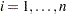, we have an unconstrained problem in which can take values in the entire 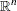space.

These different problem classes typically call for different types of algorithms to solve them. The algorithm(s) devised specifically to solve a particular class of problem might not be suitable for solving problems in a different class. For instance, there are algorithms that specifically solve unconstrained and bound constrained problems. For linearly constrained problems, the fact that the Jacobian of the constraints is constant enables us to design algorithms that are more efficient for that class.