The NETFLOW Procedure

Mathematical Description of NPSC

If a network programming problem with side constraints has n nodes, a arcs, g nonarc variables, and k side constraints, then the formal statement of the problem solved by PROC NETFLOW is

\[ \begin{array}{ll} \mr{minimize} & c^ T x + d^ T z \\ \mr{subject\ to} & F x = b \\ & H x + Q z \geq , =, \leq r \\ & l \leq x \leq u \\ & m \leq z \leq v \\ \end{array} \]

where

  • c is the 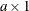$ a \times 1$ arc variable objective function coefficient vector (the cost vector)

  • x is the 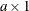$ a \times 1$ arc variable value vector (the flow vector)

  • d is the 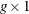$ g \times 1$ nonarc variable objective function coefficient vector

  • z is the 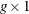$ g \times 1$ nonarc variable value vector

  • F is the 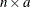$ n \times a$ node-arc incidence matrix of the network, where

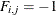    • $ F_{i,j} = -1$ if arc j is directed from node i

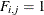    • $ F_{i,j} = 1$ if arc j is directed toward node i

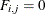    • $ F_{i,j} = 0$ otherwise

  • b is the 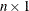$ n \times 1$ node supply/demand vector, where

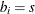    • $ b_ i = s$ if node i has supply capability of s units of flow

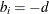    • $ b_ i = -d$ if node i has demand of d units of flow

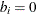    • $ b_ i = 0$ if node i is a trans-shipment node

  • H is the 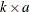$ k \times a$ side constraint coefficient matrix for arc variables, where 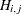$ H_{i,j}$ is the coefficient of arc j in the ith side constraint

  • Q is the 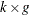$ k \times g$ side constraint coefficient matrix for nonarc variables, where 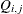$ Q_{i,j}$ is the coefficient of nonarc j in the ith side constraint

  • r is the 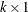$ k \times 1$ side constraint right-hand-side vector

  • l is the 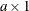$ a \times 1$ arc lower flow bound vector

  • u is the 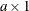$ a \times 1$ arc capacity vector

  • m is the 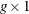$ g \times 1$ nonarc variable lower bound vector

  • v is the 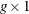$ g \times 1$ nonarc variable upper bound vector