The NETFLOW Procedure
If a network programming problem with side constraints has n nodes, a arcs, g nonarc variables, and k side constraints, then the formal statement of the problem solved by PROC NETFLOW is
![\[ \begin{array}{ll} \mr{minimize} & c^ T x + d^ T z \\ \mr{subject\ to} & F x = b \\ & H x + Q z \geq , =, \leq r \\ & l \leq x \leq u \\ & m \leq z \leq v \\ \end{array} \]](images/ormplpug_netflow0027.png)
where
-
c is the
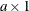 arc variable objective function coefficient vector (the cost vector)
arc variable objective function coefficient vector (the cost vector)
-
x is the
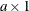 arc variable value vector (the flow vector)
arc variable value vector (the flow vector)
-
d is the
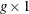 nonarc variable objective function coefficient vector
nonarc variable objective function coefficient vector
-
z is the
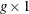 nonarc variable value vector
nonarc variable value vector
-
F is the
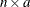 node-arc incidence matrix of the network, where
node-arc incidence matrix of the network, where
-
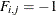 if arc j is directed from node i
if arc j is directed from node i
-
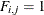 if arc j is directed toward node i
if arc j is directed toward node i
-
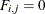 otherwise
otherwise
-
-
b is the
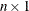 node supply/demand vector, where
node supply/demand vector, where
-
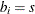 if node i has supply capability of s units of flow
if node i has supply capability of s units of flow
-
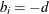 if node i has demand of d units of flow
if node i has demand of d units of flow
-
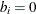 if node i is a trans-shipment node
if node i is a trans-shipment node
-
-
H is the
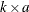 side constraint coefficient matrix for arc variables, where
side constraint coefficient matrix for arc variables, where 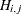 is the coefficient of arc j in the ith side constraint
is the coefficient of arc j in the ith side constraint
-
Q is the
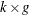 side constraint coefficient matrix for nonarc variables, where
side constraint coefficient matrix for nonarc variables, where 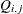 is the coefficient of nonarc j in the ith side constraint
is the coefficient of nonarc j in the ith side constraint
-
r is the
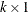 side constraint right-hand-side vector
side constraint right-hand-side vector
-
l is the
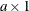 arc lower flow bound vector
arc lower flow bound vector
-
u is the
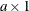 arc capacity vector
arc capacity vector
-
m is the
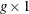 nonarc variable lower bound vector
nonarc variable lower bound vector
-
v is the
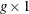 nonarc variable upper bound vector
nonarc variable upper bound vector