Introduction to Optimization
Another example helps to illustrate how the model can be simplified by exploiting the structure in the model when using the NETFLOW procedure.
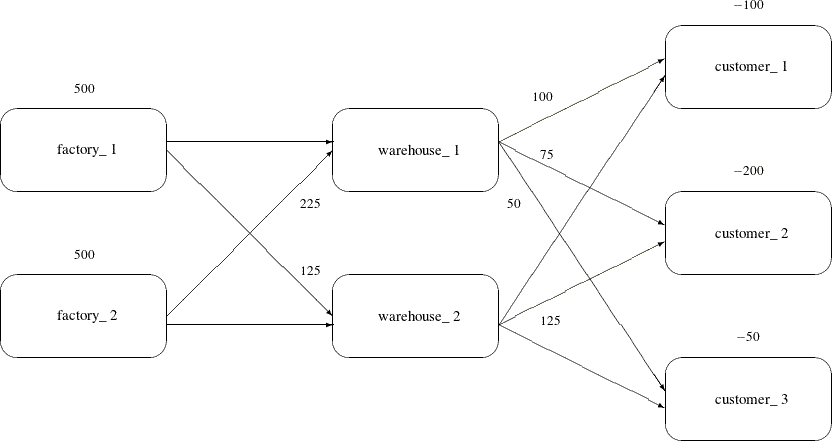
Recall the chocolate transshipment problem discussed previously. The solution required no production at factory_1 and no storage at warehouse_2. Suppose this solution, although optimal, is unacceptable. An additional constraint that requires the production at the two factories to be balanced is needed. Now, the production at the two factories can differ by, at most, 100 units. Such a constraint might look like this:
-100 <= (factory_1_warehouse_1 + factory_1_warehouse_2 -
factory_2_warehouse_1 - factory_2_warehouse_2) <= 100
The network and supply and demand information are saved in the following two data sets:
data network; format from $12. to $12.; input from $ to $ cost ; datalines; factory_1 warehouse_1 10 factory_2 warehouse_1 5 factory_1 warehouse_2 7 factory_2 warehouse_2 9 warehouse_1 customer_1 3 warehouse_1 customer_2 4 warehouse_1 customer_3 4 warehouse_2 customer_1 5 warehouse_2 customer_2 5 warehouse_2 customer_3 6 ; data nodes; format node $12. ; input node $ supdem; datalines; customer_1 -100 customer_2 -200 customer_3 -50 factory_1 500 factory_2 500 ;
The factory-balancing constraint is not a part of the network. It is represented in the sparse format in a data set for side constraints.
data side_con; format _type_ $8. _row_ $8. _col_ $21. ; input _type_ _row_ _col_ _coef_ ; datalines; eq balance . . . balance factory_1_warehouse_1 1 . balance factory_1_warehouse_2 1 . balance factory_2_warehouse_1 -1 . balance factory_2_warehouse_2 -1 . balance diff -1 lo lowerbd diff -100 up upperbd diff 100 ;
This data set contains an equality constraint that sets the value of DIFF to be the amount that factory 1 production exceeds factory 2 production. It also contains bounds on the DIFF variable. Note that the DIFF variable is a nonarc variable.
You can use the following call to PROC NETFLOW to solve the problem:
proc netflow
conout=con_sav
arcdata=network nodedata=nodes condata=side_con
sparsecondata ;
node node;
supdem supdem;
tail from;
head to;
cost cost;
run;
proc print;
var from to _name_ cost _capac_ _lo_ _supply_ _demand_
_flow_ _fcost_ _rcost_;
sum _fcost_;
run;
The solution is saved in the con_sav data set, as displayed in Figure 3.7.
Figure 3.7: CON_SAV Data Set
| Obs | from | to | _NAME_ | cost | _CAPAC_ | _LO_ | _SUPPLY_ | _DEMAND_ | _FLOW_ | _FCOST_ | _RCOST_ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | warehouse_1 | customer_1 | 3 | 99999999 | 0 | . | 100 | 100 | 300 | . | |
| 2 | warehouse_2 | customer_1 | 5 | 99999999 | 0 | . | 100 | 0 | 0 | 1.0 | |
| 3 | warehouse_1 | customer_2 | 4 | 99999999 | 0 | . | 200 | 75 | 300 | . | |
| 4 | warehouse_2 | customer_2 | 5 | 99999999 | 0 | . | 200 | 125 | 625 | . | |
| 5 | warehouse_1 | customer_3 | 4 | 99999999 | 0 | . | 50 | 50 | 200 | . | |
| 6 | warehouse_2 | customer_3 | 6 | 99999999 | 0 | . | 50 | 0 | 0 | 1.0 | |
| 7 | factory_1 | warehouse_1 | 10 | 99999999 | 0 | 500 | . | 0 | 0 | 2.0 | |
| 8 | factory_2 | warehouse_1 | 5 | 99999999 | 0 | 500 | . | 225 | 1125 | . | |
| 9 | factory_1 | warehouse_2 | 7 | 99999999 | 0 | 500 | . | 125 | 875 | . | |
| 10 | factory_2 | warehouse_2 | 9 | 99999999 | 0 | 500 | . | 0 | 0 | 5.0 | |
| 11 | diff | 0 | 100 | -100 | . | . | -100 | 0 | 1.5 | ||
| 3425 |
Notice that the solution now has production balanced across the factories; the production at factory 2 exceeds that at factory 1 by 100 units.