Restricting the Step Length :: SAS/OR(R) 12.1 User's Guide: Mathematical Programming Legacy Procedures

Restricting the Step Length

Almost all line-search algorithms use iterative extrapolation techniques which can easily lead them to (feasible) points where the objective function is no longer defined. (e.g., resulting in indefinite matrices for ML estimation) or difficult to compute (e.g., resulting in floating point overflows). Therefore, PROC NLP provides options restricting the step length $\alpha$ or trust region radius $\Delta$ , especially during the first main iterations.

The inner product of the gradient and the search direction is the slope of $f(\alpha ) = f(x + \alpha s)$ along the search direction . The default starting value $\alpha ^{(0)} = \alpha ^{(k,0)}$ in each line-search algorithm $(\min _{\alpha > 0} f(x + \alpha s))$ during the main iteration is computed in three steps:

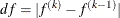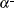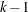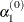The first step uses either the difference $df=|f^{(k)} - f^{(k-1)}|$ of the function values during the last two consecutive iterations or the final step length value $\alpha ^\_$ of the last iteration to compute a first value of $\alpha _1^{(0)}$ .

Not using the DAMPSTEP= option:

$\alpha _1^{(0)} = \left\{ \begin{array}{ll} \emph{step}, & \mbox{ if $0.1 \le \mi {step} \le 10$} \\[0.1in] 10, & \mbox{ if $\mi {step} > 10 $} \\[0.1in] 0.1, & \mbox{ if $\mi {step} < 0.1$} \end{array} \right.$

with

$\emph{step} = \left\{ \begin{array}{ll} df / |g^ Ts|, & \mbox{if $ |g^ Ts| \ge \epsilon \max (100\mi {df},1)$} \\[0.1in] 1, & \mbox{otherwise} \end{array} \right.$

This value of 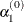$\alpha _1^{(0)}$ can be too large and lead to a difficult or impossible function evaluation, especially for highly nonlinear functions such as the EXP function.

Using the DAMPSTEP= option:

$\alpha _1^{(0)} = \min (1,r \alpha ^\_ )$

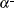The initial value for the new step length can be no larger than times the final step length $\alpha ^\_$ of the previous iteration. The default value is .

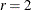During the first five iterations, the second step enables you to reduce 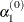$\alpha _1^{(0)}$ to a smaller starting value 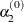$\alpha _2^{(0)}$ using the INSTEP= option:

$\alpha _2^{(0)} = \min (\alpha _1^{(0)},r)$

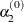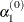After more than five iterations, $\alpha _2^{(0)}$ is set to $\alpha _1^{(0)}$ .

The third step can further reduce the step length by

$\alpha _3^{(0)} = \min (\alpha _2^{(0)},\min (10,u))$

where is the maximum length of a step inside the feasible region.

The INSTEP= option lets you specify a smaller or larger radius $\Delta$ of the trust region used in the first iteration of the trust region, double dogleg, and Levenberg-Marquardt algorithms. The default initial trust region radius $\Delta ^{(0)}$ is the length of the scaled gradient (Moré 1978). This step corresponds to the default radius factor of . In most practical applications of the TRUREG, DBLDOG, and LEVMAR algorithms, this choice is successful. However, for bad initial values and highly nonlinear objective functions (such as the EXP function), the default start radius can result in arithmetic overflows. If this happens, you may try decreasing values of INSTEP=, , until the iteration starts successfully. A small factor also affects the trust region radius $\Delta ^{(k+1)}$ of the next steps because the radius is changed in each iteration by a factor $0 < c \le 4$ , depending on the ratio $\rho$ expressing the goodness of quadratic function approximation. Reducing the radius $\Delta$ corresponds to increasing the ridge parameter $\lambda$ , producing smaller steps directed more closely toward the (negative) gradient direction.