MINQUAD and MAXQUAD Statements :: SAS/OR(R) 12.1 User's Guide: Mathematical Programming Legacy Procedures

MINQUAD and MAXQUAD Statements

MINQUAD H_name [ , g_name [ , c_number ] ] ;

MAXQUAD H_name [ , g_name [ , c_number ] ] ;

The MINQUAD and MAXQUAD statements specify the matrix , vector , and scalar that define a quadratic objective function. The MINQUAD statement is for minimizing the objective function and the MAXQUAD statement is for maximizing the objective function.

The rows and columns in and correspond to the order of decision variables given in the DECVAR statement. Specifying the objective function with a MINQUAD or MAXQUAD statement indirectly defines the analytic derivatives for the objective function. Therefore, statements specifying derivatives are not valid in these cases. Also, only use these statements when TECH=LICOMP or TECH=QUADAS and no nonlinear constraints are imposed.

There are three ways of using the MINQUAD or MAXQUAD statement:

Using ARRAY Statements: The names H_name and g_name specified in the MINQUAD or MAXQUAD statement can be used in ARRAY statements. This specification is mainly for small problems with almost dense 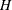matrices.
```
proc nlp pall;
   array h[2,2] .4 0
                 0 4;
   minquad h, -100;
   decvar x1 x2 = -1;
   bounds  2 <= x1 <= 50,
         -50 <= x2 <= 50;
   lincon 10 <= 10 * x1 - x2;
run;
```
Using Elementwise Setting: The names H_name and g_name specified in the MINQUAD or MAXQUAD statement can be followed directly by one-dimensional indices specifying the corresponding elements of the matrix 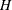and vector 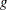. These element names can be used on the left side of numerical assignments. The one-dimensional index value 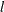following H_name, which corresponds to the element 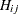$H_{ij}$ , is computed by 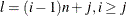$l = (i-1)n + j, i \geq j$ . The matrix 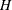and vector 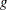are initialized to zero, so that only the nonzero elements must be given. This specification is efficient for small problems with sparse 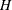matrices.
```
proc nlp pall;
   minquad h, -100;
   decvar x1 x2;
   bounds  2 <= x1 <= 50,
         -50 <= x2 <= 50;
   lincon 10 <= 10 * x1 - x2;
   h1 = .4; h4 = 4;
run;
```
Using MATRIX Statements: The names H_name and g_name specified in the MINQUAD or MAXQUAD statement can be used in MATRIX statements. There are different ways to specify the nonzero elements of the matrix 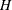and vector 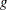by MATRIX statements. The following example illustrates one way to use the MATRIX statement.
```
proc nlp all;
   matrix h[1,1] = .4 4;
   minquad h, -100;
   decvar x1 x2 = -1;
   bounds 2 <= x1 <= 50,
        -50 <= x2 <= 50;
   lincon 10 <= 10 * x1 - x2;
run;
```