Mathematical Description of NPSC
If a network programming problem with side constraints has ![]() nodes,
nodes, ![]() arcs,
arcs, ![]() nonarc variables, and
nonarc variables, and ![]() side constraints, then the formal statement of the problem solved by PROC NETFLOW is
side constraints, then the formal statement of the problem solved by PROC NETFLOW is
![\[ \begin{array}{ll} \mr {minimize} & c^ T x + d^ T z \\ \mr {subject\ to} & F x = b \\ & H x + Q z \geq , =, \leq r \\ & l \leq x \leq u \\ & m \leq z \leq v \\ \end{array} \]](images/ormplpug_netflow0037.png) |
where
-
 is the
is the 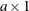 arc variable objective function coefficient vector (the cost vector)
arc variable objective function coefficient vector (the cost vector)
-
 is the
is the 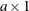 arc variable value vector (the flow vector)
arc variable value vector (the flow vector)
-
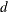 is the
is the 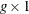 nonarc variable objective function coefficient vector
nonarc variable objective function coefficient vector
-
 is the
is the 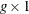 nonarc variable value vector
nonarc variable value vector
-
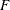 is the
is the 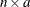 node-arc incidence matrix of the network, where
node-arc incidence matrix of the network, where
-
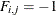 if arc
if arc 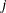 is directed from node
is directed from node 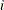
-
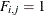 if arc
if arc 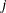 is directed toward node
is directed toward node 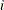
-
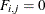 otherwise
otherwise
-
-
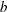 is the
is the 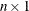 node supply/demand vector, where
node supply/demand vector, where
-
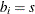 if node
if node 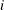 has supply capability of
has supply capability of  units of flow
units of flow
-
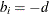 if node
if node 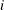 has demand of
has demand of 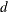 units of flow
units of flow
-
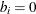 if node
if node 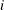 is a trans-shipment node
is a trans-shipment node
-
-
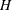 is the
is the 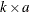 side constraint coefficient matrix for arc variables, where
side constraint coefficient matrix for arc variables, where 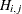 is the coefficient of arc
is the coefficient of arc 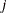 in the
in the 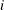 th side constraint
th side constraint
-
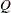 is the
is the 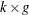 side constraint coefficient matrix for nonarc variables, where
side constraint coefficient matrix for nonarc variables, where 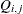 is the coefficient of nonarc
is the coefficient of nonarc 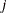 in the
in the 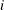 th side constraint
th side constraint
-
 is the
is the 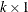 side constraint right-hand-side vector
side constraint right-hand-side vector
-
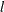 is the
is the 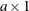 arc lower flow bound vector
arc lower flow bound vector
-
 is the
is the 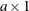 arc capacity vector
arc capacity vector
-
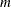 is the
is the 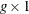 nonarc variable lower bound vector
nonarc variable lower bound vector
-
 is the
is the 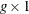 nonarc variable upper bound vector
nonarc variable upper bound vector