The rows and columns of the Hessian and crossproduct Jacobian matrix can be scaled when using the trust region, Newton-Raphson, double dogleg, and Levenberg-Marquardt optimization techniques. Each element , 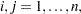is divided by the scaling factor , where the scaling vector 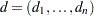is iteratively updated in a way specified by the HESCAL= option, as follows:

• No scaling is done (equivalent to ).

• First iteration and each restart iteration:

• refer to Moré (1978):

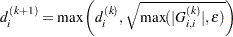
• refer to Dennis, Gay, and Welsch (1981):

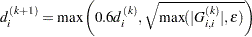
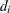• is reset in each iteration: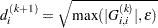

where is the relative machine precision or, equivalently, the largest double precision value that when added to 1 results in 1.