| JACOBIAN Statement |
The JACOBIAN statement defines the JACOBIAN matrix  for a system of objective functions. For more information, see the section Derivatives.
for a system of objective functions. For more information, see the section Derivatives.
The JACOBIAN statement lists  variable names that correspond to the elements
variable names that correspond to the elements 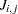 ,
,  , of the Jacobian matrix listed by rows.
, of the Jacobian matrix listed by rows.
For example, the statements
lsq f1-f3; decvar x1 x2; jacobian j1-j6;
correspond to the Jacobian matrix
 |
The  rows of the Jacobian matrix must correspond to the order of the
rows of the Jacobian matrix must correspond to the order of the  function names listed in the MIN, MAX, or LSQ statement. The
function names listed in the MIN, MAX, or LSQ statement. The  columns of the Jacobian matrix must correspond to the order of the
columns of the Jacobian matrix must correspond to the order of the  decision variables listed in the DECVAR statement. To specify the values of nonzero derivatives, the variables specified in the JACOBIAN statement must be defined on the left-hand side of algebraic expressions in programming statements.
decision variables listed in the DECVAR statement. To specify the values of nonzero derivatives, the variables specified in the JACOBIAN statement must be defined on the left-hand side of algebraic expressions in programming statements.
For example, consider the Rosenbrock function:
proc nlp tech=levmar; array j[2,2] j1-j4; lsq f1 f2; decvar x1 x2; jacobian j1-j4; f1 = 10 * (x2 - x1 * x1); f2 = 1 - x1; j[1,1] = -20 * x1; j[1,2] = 10; j[2,1] = -1; j[2,2] = 0; /* is not needed */ run;
The JACOBIAN statement is useful only if more than one objective function is given in the MIN, MAX, or LSQ statement, or if a DATA= input data set specifies more than one function. If the MIN, MAX, or LSQ statement contains only one objective function and no DATA= input data set is used, the JACOBIAN and GRADIENT statements are equivalent. In the case of least squares minimization, the crossproduct Jacobian is used as an approximate Hessian matrix.