PROC NLP: CRPJAC Statement

CRPJAC Statement

CRPJAC variables ;

The CRPJAC statement defines the crossproduct Jacobian matrix 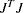$\text{[math]}$ used in solving least squares problems. For more information, see the section Derivatives. If the DIAHES option is not specified, the CRPJAC statement lists 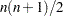$\text{[math]}$ variable names, which correspond to the elements 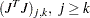$\text{[math]}$ of the lower triangle of the symmetric crossproduct Jacobian matrix listed by rows. For example, the statements

   lsq f1-f3;
   decvar x1-x3;
   crpjac jj1-jj6;

correspond to the crossproduct Jacobian matrix

$\text{[math]}$

If the DIAHES option is specified, only the $\text{[math]}$ diagonal elements must be listed in the CRPJAC statement. The $\text{[math]}$ rows and $\text{[math]}$ columns of the crossproduct Jacobian matrix must be in the same order as the $\text{[math]}$ corresponding parameter names listed in the DECVAR statement. To specify the values of nonzero derivatives, the variables specified in the CRPJAC statement have to be defined at the left-hand side of algebraic expressions in programming statements. For example, consider the Rosenbrock function:

proc nlp tech=levmar;
   lsq f1 f2;
   decvar x1 x2;
   gradient g1 g2;
   crpjac cpj1-cpj3;
   
   f1   = 10 * (x2 - x1 * x1);
   f2   = 1 - x1;
   g1   = -200 * x1 * (x2 - x1 * x1) - (1 - x1);
   g2   =  100 * (x2 - x1 * x1);
   
   cpj1 = 400 * x1 * x1 + 1 ;
   cpj2 = -200 * x1;
   cpj3 = 100;
run;