Lost Baggage Distribution

The following constraints are used in this example:

bounds on variables
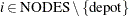for $i \in \text {NODES} \setminus \{ \text {depot}\}$ ,

$\sum _{v \in \text {VEHICLES}} \Variable{UseNode[i,v]} = 1$
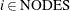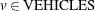for $i \in \text {NODES}$ and $v \in \text {VEHICLES}$ ,

$\sum _{(i,j) \in \text {ARCS}} \Variable{UseArc[i,j,v]} = \Variable{UseNode[i,v]}$
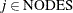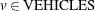for $j \in \text {NODES}$ and $v \in \text {VEHICLES}$ ,

$\sum _{(i,j) \in \text {ARCS}} \Variable{UseArc[i,j,v]} = \Variable{UseNode[j,v]}$
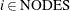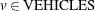for $i \in \text {NODES}$ and $v \in \text {VEHICLES}$ ,

$\Variable{UseNode[i,v]} \le \Variable{UseVehicle[v]}$
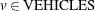for $v \in \text {VEHICLES}$ ,

$\Variable{UseVehicle[v]} \le \Variable{UseNode[depot,v]}$
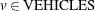for $v \in \text {VEHICLES}$ ,

$\Variable{TimeUsed[v]} = \sum _{(i,j) \in \text {ARCS}} \Argument{travel\_ time[i,j]} \cdot \Variable{UseArc[i,j,v]}$
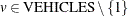for $v \in \text {VEHICLES} \setminus \{ 1\}$ ,

$\sum _{i \in \text {NODES}} \Variable{UseNode[i,v]} \le \sum _{i \in \text {NODES}} \Variable{UseNode[i,v}-\Variable{1]}$
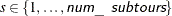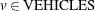for $s \in \{ 1, \dots , \Argument{num\_ subtours}\}$ and $k \in \text {SUBTOUR[s]}$ and $v \in \text {VEHICLES}$ ,

$\sum _{\substack{i \in \text {NODES} \setminus \text {SUBTOUR[s]},\\ j \in \text {SUBTOUR[s]}:\\ (i,j) \in \text {ARCS}}} \Variable{UseArc[i,j,v]} + \sum _{\substack{i \in \text {SUBTOUR[s]},\\ j \in \text {NODES} \setminus \text {SUBTOUR[s]}:\\ (i,j) \in \text {ARCS}}} \Variable{UseArc[i,j,v]} \ge 2 \cdot \Variable{UseNode[k,v]}$
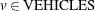for $v \in \text {VEHICLES}$ ,

$\Variable{MaxTimeUsed} \ge \Variable{TimeUsed[v]}$