Three-Dimensional Noughts and Crosses: A Combinatorial Problem

The following constraints are used in this example:

bounds on variables
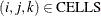for $(i,j,k) \in \text {CELLS}$ ,

$\sum _{\text {color} \in \text {COLORS}} \Variable{IsColor[i,j,k,color]} = 1$
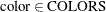for $\text {color} \in \text {COLORS}$ ,

$\sum _{(i,j,k) \in \text {CELLS}} \Variable{IsColor[i,j,k,color]} = \Argument{num\_ balls[color]}$
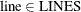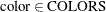for $\text {line} \in \text {LINES}$ and $\text {color} \in \text {COLORS}$ ,

$\sum _{(i,j,k) \in \mr{CELLS\_ line[line]}} \Variable{IsColor[i,j,k,color]} - \left|\mr{CELLS\_ line[line]}\right| + 1 \le \Variable{IsMonochromatic[line]}$