Curve Fitting: Fitting a Curve to a Set of Data Points

Problem Statement

A quantity y is known to depend upon another quantity x.[12] A set of corresponding values has been collected for x and y and is presented in Table 11.1.

Table 11.1:

x

0.0

0.5

1.0

1.5

1.9

2.5

3.0

3.5

4.0

4.5

y

1.0

0.9

0.7

1.5

2.0

2.4

3.2

2.0

2.7

3.5

x

5.0

5.5

6.0

6.6

7.0

7.6

8.5

9.0

10.0

 

y

1.0

4.0

3.6

2.7

5.7

4.6

6.0

6.8

7.3

 


  1. Fit the ‘best’ straight line 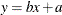$y = bx + a$ to this set of data points. The objective is to minimize the sum of absolute deviations of each observed value of y from the value predicted by the linear relationship.

  2. Fit the ‘best’ straight line where the objective is to minimize the maximum deviation of all the observed values of y from the value predicted by the linear relationship.

  3. Fit the ‘best’ quadratic curve 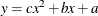$y = cx^2 + bx + a$ to this set of data points using the same objectives as in (1) and (2).


[12] Reproduced with permission of John Wiley & Sons Ltd. (Williams 1999, pp. 242–243).