Decentralization: How to Disperse Offices from the Capital
Constraints
The following constraints are used in this example:
-
bounds on variables
-
![$\displaystyle { \Variable{TotalBenefit} = \sum _{i \in \text {DEPTS}} \sum _{j \in \text {CITIES}} \Argument{benefit[i,j]} \cdot \Variable{Assign[i,j]} }$](images/ormpex_ex100010.png)
-
![$\displaystyle { \Variable{TotalCost} = \sum _{(i,j,k,l) \in \text {IJKL}} \Argument{comm[i,k]} \cdot \Argument{cost[j,l]} \cdot \Variable{Product[i,j,k,l]} }$](images/ormpex_ex100011.png)
-
for
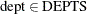 ,
,
![\[ \sum _{\text {city} \in \text {CITIES}} \Variable{Assign[dept,city]} = 1 \]](images/ormpex_ex100013.png)
-
for
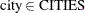 ,
,
![\[ \sum _{\text {dept} \in \text {DEPTS}} \Variable{Assign[dept,city]} \le \Argument{max\_ num\_ depts} \]](images/ormpex_ex100015.png)
-
for
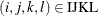 ,
,
![\[ \Variable{Assign[i,j]} + \Variable{Assign[k,l]} - 1 \le \Variable{Product[i,j,k,l]} \]](images/ormpex_ex100017.png)
-
for
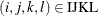 ,
,
![\[ \Variable{Product[i,j,k,l]} \le \Variable{Assign[i,j]} \]](images/ormpex_ex100018.png)
-
for
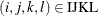 ,
,
![\[ \Variable{Product[i,j,k,l]} \le \Variable{Assign[k,l]} \]](images/ormpex_ex100019.png)
-
for
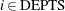 and
and 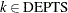 and
and 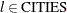 such that
such that 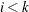 ,
,
![\[ \sum _{(i,j,k,l) \in \text {IJKL}} \Variable{Product[i,j,k,l]} = \Variable{Assign[k,l]} \]](images/ormpex_ex100024.png)
-
for
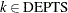 and
and 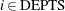 and
and 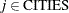 such that
such that 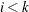 ,
,
![\[ \sum _{(i,j,k,l) \in \text {IJKL}} \Variable{Product[i,j,k,l]} = \Variable{Assign[i,j]} \]](images/ormpex_ex100026.png)