Protein Comparison

Problem Statement

This problem is also based on one in the paper by Forrester and Greenberg (2008).[30] It is concerned with measuring the similarities of two proteins. A protein can be represented by an (undirected) graph with the acids represented by the nodes and the edges being present when two acids are within a threshold distance of each other. This graphical representation is known as the contact map of the protein. Given two contact maps, representing proteins, we would like to find the largest (measured by number of corresponding edges) isomorphic subgraphs in each graph. The acids in each of the proteins are ordered. 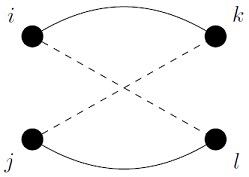We need to preserve this ordering in each of the subgraphs, which implies that there can be no crossovers in the comparison. This is illustrated in Figure 29.1. If $i < k$ in the contact map for the first protein then we cannot have $l < j$ in the second protein, if i is to be associated with j and k with l in the comparison.

Figure 29.1:  

fig12_11


This problem is well known for being very difficult to solve for even modestly sized proteins.

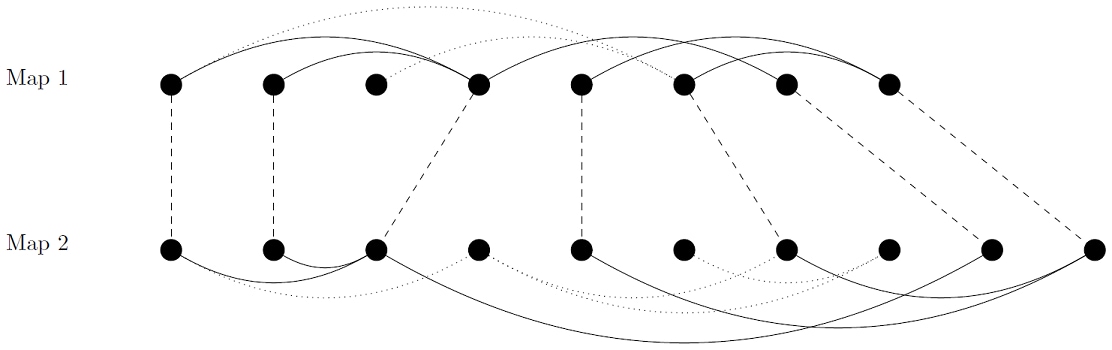
In Figure 29.2, we give an optimal comparison between two small contact maps leading to 5 corresponding edges.

Figure 29.2:  

fig12_12


The problem we present here is to compare the contact maps given in Figure 29.3 and Figure 29.4.

Figure 29.3:  

fig12_13


Figure 29.4:  

fig12_14



[30] Reproduced with permission of John Wiley & Sons Ltd. (Williams 2013, pp. 290–291).