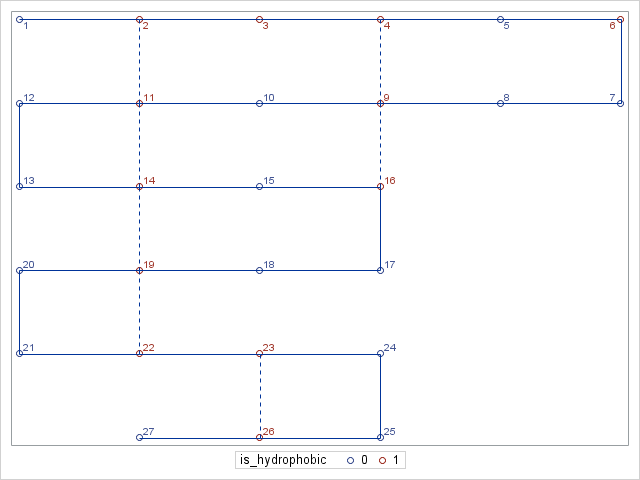
This problem is based on one in the paper by Forrester and Greenberg (2008).[29] It is a simplification of a problem in molecular biology. We take a protein as consisting of a chain of amino acids. For the purpose of this problem, the amino acids come in two forms: hydrophilic (water-loving) and hydrophobic (water-hating). An example of such a chain is given in Figure 28.1, with the hydrophobic acids marked in bold.

Such a chain naturally folds so as to bring as many hydrophobic acids as possible close together. An optimum folding for the chain, in two dimensions, is given in Figure 28.2, with the new matches marked by dashed lines. The problem is to predict the optimum folding. (Forrester and Greenberg also impose a condition that the resultant protein be confined to a given lattice of points. We do not impose that condition here). This problem can be modelled by a number of integer programming formulations. Some of these are discussed in the above reference. Another formulation is suggested in section 13.28 [of Williams (2013)]. The problem posed here is to find the optimum folding for a chain of 50 amino acids with hydrophobic acids at positions 2, 4, 5, 6, 11, 12, 17, 20, 21, 25, 27, 28, 30, 31, 33, 37, 44 and 46 as shown in Figure 28.3.