 |
|
| The CLP Procedure |
Example 3.4 A Nonlinear Optimization Problem
This example illustrates how you can use the element constraint to represent almost any function between two variables in addition to representing nonstandard domains. Consider the following nonlinear optimization problem:
 |
 |
|
|||
|
 |
 |
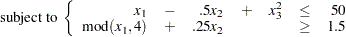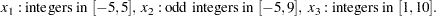You can use the CLP procedure to solve this problem by introducing four artificial variables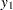 
–
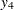to represent each of the nonlinear terms. Let 
, 
, 
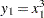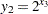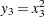, and 
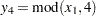. Since the domains of 
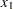and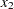 
are not consecutive integers that start from 1, you can use element constraints to represent their domains by using index variables 
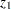and 
, respectively. For example, either of the following two ELEMENT constraints specifies that the domain of 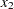is the set of odd integers in 
:
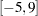element(z2,(-5,-3,-1,1,3,5,7,9),x2) element(z2,(-5 to 9 by 2),x2)
Any functional dependencies on 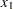or 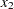can now be defined using 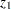or , respectively, as the index variable in an element constraint. Since the domain of 
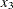is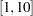 
, you can directly use 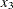as the index variable in an element constraint to define dependencies on .
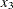For example, the following constraint specifies the function ,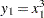 
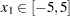
element(z1,(-125,-64,-27,-8,-1,0,1,8,27,64,125),y1)
The nonlinear optimization problem can now be reduced to a set of element and linear constraints. By expressing the objective function as a linear constraint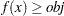 
where obj is a supplied parameter, you can find a solution with objective value of at least obj.
In a manner similar to that of Example 3.3, you can create a SAS macro %CALLCLP with parameter obj that can be called iteratively from a search method such as %FINDMAX to determine the optimal value of the objective function, as follows:
%macro callclp(obj);
%put The objective value is: &obj..;
proc clp out=clpout;
var x1=[-5, 5] x2=[-5, 9] x3=[1, 10] (y1-y4) (z1-z2);
/* Use element constraint to represent non-contiguous domains */
/* and nonlinear functions. */
element
/* Domain of x1 is [-5,5] */
(z1, ( -5 to 5), x1)
/* Functional Dependencies on x1 */
/* y1 = x1^3 */
(z1, (-125, -64, -27, -8, -1, 0, 1, 8, 27, 64, 125), y1)
/* y4 = mod(x1, 4) */
(z1, ( -1, 0, -3, -2, -1, 0, 1, 2, 3, 0, 1), y4)
/* Domain of x2 is the set of odd numbers in [-5, 9] */
(z2, (-5 to 9 by 2), x2)
/* Functional Dependencies on x3 */
/* y2 = 2^x3 */
(x3, (2, 4, 8, 16, 32, 64, 128, 256, 512, 1024), y2)
/* y3 = x3^2 */
(x3, (1, 4, 9, 16, 25, 36, 49, 64, 81, 100), y3);
lincon
/* Objective function: x1^3 + 5 * x2 - 2^x3 */
y1 + 5 * x2 - y2 >= &obj,
/* x1 - .5 * x2 + x3^2 <=50 */
x1 - .5 * x2 + y3 <= 50,
/* mod(x1, 4) + .25 * x2 >= 1.5 */
y4 + .25 * x2 >= 1.5;
run;
/* when a solution is found, */
/* &_ORCLP_ contains the string SOLUTIONS_FOUND */
%if %index(&_ORCLP_, SOLUTIONS_FOUND) %then %let clpreturn=SUCCESSFUL;
%mend;
/* Bisection search to determine the optimal objective value. */
%macro findmax(lb, ub);
%do %while (&lb<&ub-1);
%put Currently lb=&lb, ub=&ub..;
%let newobj=%eval((&lb+&ub)/2);
%let clpreturn=NOTFOUND;
%callclp(&newobj);
%if &clpreturn=SUCCESSFUL %then %let lb=&newobj;
%else %let ub=&newobj;
%end;
%callclp(&lb);
%put Maximum possible objective value within given range is &lb.;
%put Any value greater than &lb makes the problem infeasible.;
proc print;
run;
%mend;
/*Find the maximum objective value between -200 and 200. */
%findmax(lb=-200, ub=200);
Output 3.4.1 shows the solution that corresponds to the optimal objective value of 168.
|
|
Copyright © SAS Institute, Inc. All Rights Reserved.