An element_constraint is specified in the following form:

(index variable, (integer list), variable)

The ELEMENT statement specifies one or more element constraints. An element constraint enables you to define dependencies, not necessarily functional, between variables. The statement

  ELEMENT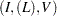

sets the variable 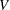to be equal to the 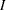th element in the list 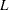. The list of integers 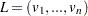is a list of values that the variable 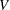can take and are not necessarily distinct. The variable 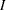is the index variable and its domain is considered to be 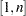. Each time the domain of 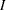is modified, the domain of 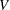is updated and vice versa.

An element constraint enforces the following propagation rules:

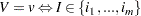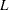where is a value in the list and 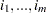are all the indices in 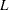whose value is .

The following statements use the element constraint to implement the quadratic function :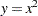

proc clp out=clpout;
   var x=[1,5] y=[1,25];
   element (x,(1, 4, 9, 16, 25), y);
run;

An element constraint is equivalent to a conjunction of reify and linear constraints. For example, the preceding statements are equivalent to:

proc clp out=clpout;
        var x=[1,5] y=[1,25] (R1-R5)=[0,1];
        reify R1: (x=1);
        reify R1: (y=1);
        reify R2: (x=2);
        reify R2: (y=4);
        reify R3: (x=3);
        reify R3: (y=9);
        reify R4: (x=4);
        reify R4: (y=16);
        reify R5: (x=5);
        reify R5: (y=25);
        lincon R1 + R2 + R3 + R4 + R5 = 1;
run;

Element constraints can also be used to define positional mappings between two variables. For example, suppose the function 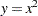is defined on only odd numbers in the interval 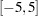. You can model this by using two element constraints and an artificial index variable:

   element (i, ( -5, -3, -1, 1, 3,  5), x)
           (i, ( 25,  9,  1, 1, 9, 25), y);

The list of values L can also be specified by using a convenient syntax of the form start TO end or start TO end BY increment. For example, the previous element specification is equivalent to:

   element (i, ( -5 to 5 by 2), x)
           (i, ( 25,  9,  1, 1, 9, 25), y);