MSPLINT Function
Returns the ordinate of a monotonicity-preserving interpolating spline.
| Category: | Mathematical |
Syntax
Required Arguments
X
is a numeric constant, variable, or expression that specifies the abscissa for which the ordinate of the spline is to be computed.
n
is a numeric constant, variable, or expression that specifies the number of knots. N must be a positive integer.
X1, …, Xn
are numeric constants, variables, or expressions that specify the abscissas of the knots. These values must be non-missing and listed in nondecreasing order. Otherwise, the result is undefined. MSPLINT does not check the order of the X1 through Xn arguments.
Y1, ..., Yn
are numeric constants, variables, or expressions that specify the ordinates of the knots. The number of Y1 through Yn arguments must be the same as the number of X1 throughXn arguments.
Details
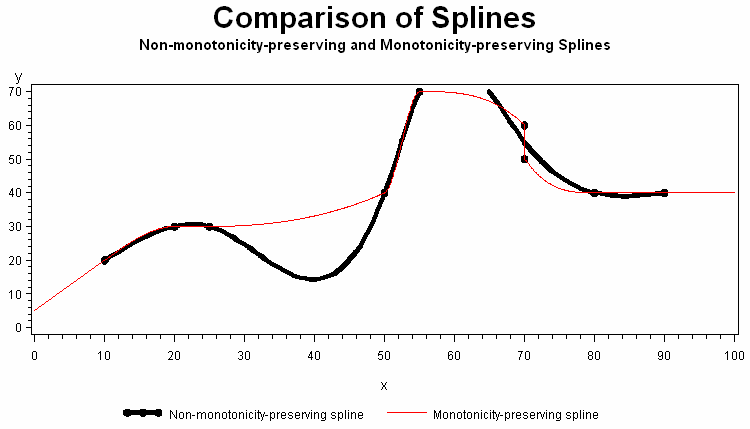
Example
data msplint;
do x=0 to 100 by .1;
msplint=msplint(x, 9,
10, 20, 25, 50, 55, 70, 70, 80, 90,
20, 30, 30, 40, 70, 60, 50, 40, 40);
output;
end;
run;
data knots;
input x y;
datalines;
10 20
20 30
25 30
50 40
55 70
70 60
70 50
80 40
90 40
;
data plot;
merge knots msplint;
by x;
run;
title "Comparison of Splines";
title2 "Non-monotonicity-preserving and Monotonicity-preserving
Splines";
legend1 value=('Non-monotonicity-preserving spline'
'Monotonicity-preserving spline') label=none;
symbol1 value=dot interpol=spline color=black width=5;
symbol2 value=none interpol=join color=red;
proc gplot data=plot;
plot y*x=1 msplint*x=2/overlay legend=legend1;
run;
quit;