Using Random-Number Functions and CALL Routines
Types of Random-Number Functions
Two types of random-number
functions are available in SAS. The newest random-number function
is the RAND function. It uses the Mersenne-Twister pseudo-random number
generator (RNG) that was developed by Matsumoto and Nishimura (1998).
This RNG has a very long period of 219937 –
1, and has very good statistical properties. (A period is the number
of occurrences before the pseudo-random number sequence repeats.)
The RAND function is
started with a single seed. However, the state of the process cannot
be captured by a single seed, which means that you cannot stop and
restart the generator from its stopping point. Use the STREAMINIT
function to produce a sequence of values that begins at the beginning
of a stream. For more information,
see the Details section of the RAND Function.
The older random-number
generators include the UNIFORM, NORMAL, RANUNI, RANNOR, and other
functions that begin with RAN. These functions have a period of only
231 – 2 or less. The pseudo-random
number stream is started with a single seed, and the state of the
process can be captured in a new seed. This means that you can stop
and restart the generator from its stopping point by providing the
proper seed to the corresponding CALL routines. You can use the random-number
functions to produce a sequence of values that begins in the middle
of a stream.
Seed Values
Random-number
functions and CALL routines generate streams of pseudo-random numbers
from an initial starting point, called a seed,
that either the user or the computer clock supplies. A seed must be
a nonnegative integer with a value less than 231–1
(or 2,147,483,647). If you use a positive seed, you can always replicate
the stream of random numbers by using the same DATA step. If you use
zero as the seed, the computer clock initializes the stream, and the
stream of random numbers cannot be replicated.
Understanding How Functions Generate a Random-Number Stream
Using the DATA Step to Generate a Single Stream of Random Numbers
The
DATA steps in this section illustrate several properties of the random-number
functions. Each of the DATA steps that call a function generates a
single stream of pseudo-random numbers based on a seed value of 7,
because that is the first seed for the first call for every step.
Some of the DATA steps change the seed value in various ways. Some
of the steps have single function calls and others have multiple function
calls. None of these DATA steps change the seed. The only seed that
is relevant to the function calls is the seed that was used with the
first execution of the first random-number function. There is no way
to create separate streams with functions (CALL routines are used
for this purpose), and the only way that you can restart the function
random-number stream is to start a new DATA step.
The following example
executes multiple DATA steps:
/* This DATA step produces a single stream of random numbers */
/* based on a seed value of 7. */
data a;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
a = ranuni (7); output;
run;
/* This DATA step uses a DO statement to produce a single */
/* stream of random numbers based on a seed value of 7. */
data b (drop = i);
do i = 7 to 18;
b = ranuni (i);
output;
end;
run;
/* This DATA step uses a DO statement to produce a single */
/* stream of random numbers based on a seed value of 7. */
data c (drop = i);
do i = 1 to 12;
c = ranuni (7);
output;
end;
run;
/* This DATA step calls the RANUNI and the RANNOR functions */
/* and produces a single stream of random numbers based on */
/* a seed value of 7. */
data d;
d = ranuni (7); f = ' '; output;
d = ranuni (8); f = ' '; output;
d = rannor (9); f = 'n'; output;
d = .; f = ' '; output;
d = ranuni (0); f = ' '; output;
d = ranuni (1); f = ' '; output;
d = rannor (2); f = 'n'; output;
d = .; f = ' '; output;
d = ranuni (3); f = ' '; output;
d = ranuni (4); f = ' '; output;
d = rannor (5); f = 'n'; output;
d = .; f = ' '; output;
run;
/* This DATA step calls the RANNOR function and produces a */
/* single stream of random numbers based on a seed value of 7. */
data e (drop = i);
do i = 1 to 6;
e = rannor (7); output;
e = .; output;
end;
run;
/* This DATA step merges the output data sets that were */
/* created from the previous five DATA steps. */
data five;
merge a b c d e;
run;
/* This procedure writes the output from the merged data sets. */
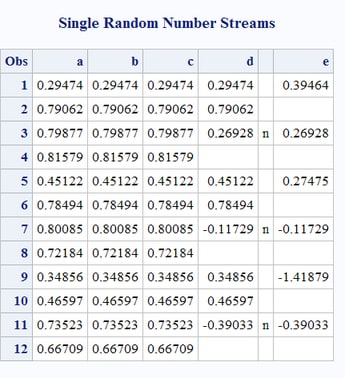
proc print label data=five;
options missing = ' ';
label f = '00'x;
title 'Single Random Number Streams';
run;The pseudo-random number
streams in output data sets A, B, and C are identical. The stream
in output data set D mixes calls to the RANUNI and the RANNOR functions.
In observations 1, 2, 5, 6, 9, and 10, the values that are returned
by RANUNI exactly match the values in the previous streams. Observations
3, 7, and 11, which are flagged by “n”, contain the
values that are returned by the RANNOR function. The mix of the function
calls does not affect the generation of the pseudo-random number stream.
All of the results are based on a single stream of uniformly distributed
values, some of which are transformed and returned from other functions
such as RANNOR. The results of the RANNOR function are produced from
two internal calls to RANUNI. The DATA step that creates output data
set D executes the following steps three times to create 12 observations:
In the DATA step that
creates data set E, RANNOR is called six times, each time skipping
a line to compensate for the fact that two internal calls to RANUNI
are made for each call to RANNOR. Notice that the three values that
are returned from RANNOR in the DATA step that creates data set D
match the corresponding values in data set E.
Using the %SYSFUNC Macro to Generate a Single Stream of Random Numbers
When
the RANUNI function is called through the macro language by using
%SYSFUNC, one pseudo-random number stream is created. You cannot change
the seed value unless you close SAS and start a new SAS session. The
%SYSFUNC macro produces the same pseudo-random number stream as the
DATA steps that generated the data sets A, B, and C for the first
macro invocation only. Any subsequent macro calls produce a continuation
of the single stream.
Results of Execution with the %SYSFUNC Macro
10 %macro ran; 11 %do i = 1 %to 12; 12 %let x = %sysfunc (ranuni (7)); 13 %put &x; 14 %end; 15 %mend; 16 %ran; 0.29473798875451 0.79062100955779 0.79877014262544 0.81579051763554 0.45121804506109 0.78494144826426 0.80085421204606 0.72184205973606 0.34855818345609 0.46596586120592 0.73522999404707 0.66709365028287
Comparison of Seed Values in Random-Number Functions and CALL Routines
Each random-number function
and CALL routine generates pseudo-random numbers from a specific statistical
distribution. Each random-number function requires a seed value expressed
as an integer constant or a variable that contains the integer constant.
Each CALL routine calls a variable that contains the seed value. Additionally,
every CALL routine requires a variable that contains the generated
pseudo-random numbers.
The seed variable must
be initialized before the first execution of the function or CALL
routine. After each execution of a function, the current seed is updated
internally, but the value of the seed argument remains unchanged.
However, after each iteration of the CALL routine the seed variable
contains the current seed in the stream that generates the next pseudo-random
number. With a function, it is not possible to control the seed values,
and, therefore, the pseudo-random numbers after the initialization.
Generating Multiple Streams from Multiple Seeds in Random-Number CALL Routines
Overview of Random-Number CALL Routines and Streams
You can use the random-number
CALL routines to generate multiple streams of pseudo-random numbers
within a single DATA step. If you supply a different seed value to
initialize each of the seed variables, the streams of the generated
pseudo-random numbers are computationally independent, but they might
not be statistically independent unless you select the seed values
carefully.
Example 1: Using Multiple Seeds to Generate Multiple Streams
This example shows that
you can use multiple seeds to generate multiple streams of pseudo-randomly
distributed values by using the random-number CALL routines. The first
DATA step creates a data set with three variables that are normally
distributed. The second DATA step creates variables that are uniformly
distributed. The SGSCATTER procedure (see the SAS ODS Graphics: Procedures Guide ) is used to show the relationship between each pair
of variables for each of the two distributions.
data normal;
seed1 = 11111;
seed2 = 22222;
seed3 = 33333;
do i = 1 to 10000;
call rannor(seed1, x1);
call rannor(seed2, x2);
call rannor(seed3, x3);
output;
end;
run;
data uniform;
seed1 = 11111;
seed2 = 22222;
seed3 = 33333;
do i = 1 to 10000;
call ranuni(seed1, x1);
call ranuni(seed2, x2);
call ranuni(seed3, x3);
output;
end;
run;
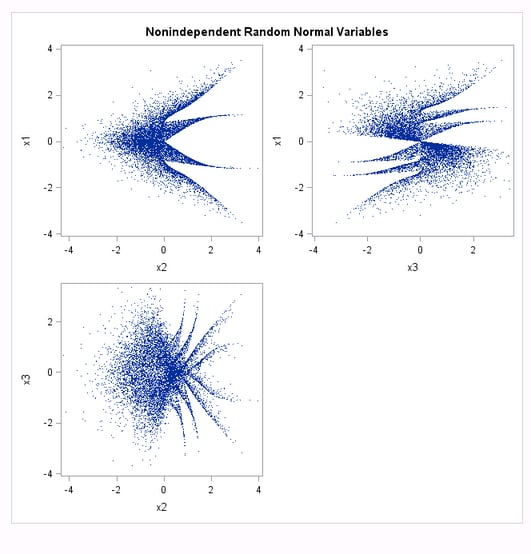
proc sgscatter data = normal;
title 'Nonindependent Random Normal Variables';
plot x1*x2 x1*x3 x3*x2 / markerattrs = (size = 1);
run;
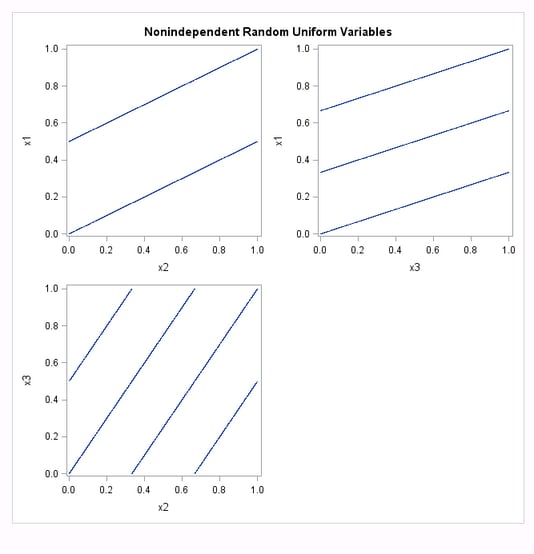
proc sgscatter data = uniform;
title 'Nonindependent Random Uniform Variables';
plot x1*x2 x1*x3 x3*x2 / markerattrs = (size = 1);
run;
The first plot (
Multiple Streams from Multiple Seeds: Nonindependent Random Normal Variables) shows that normal variables appear to be linearly uncorrelated,
but they are obviously not independent. The second plot ( Multiple Streams from Multiple Seeds: Nonindependent Random Uniform Variables) shows that uniform variables are clearly related. With
this class of random-number generators, there is never any guarantee
that the streams will be independent.
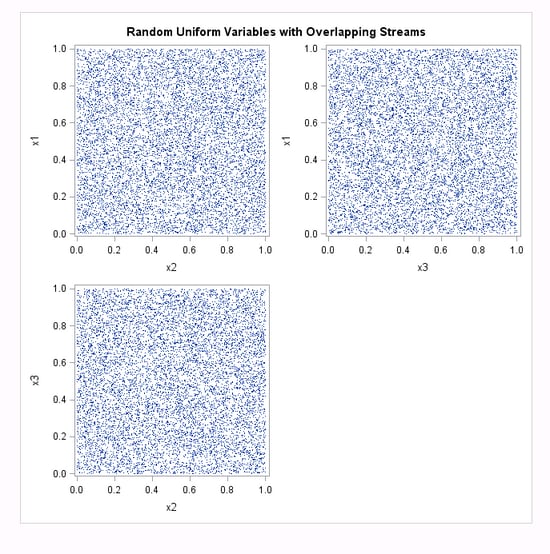
Example 2: Using Different Seeds with the CALL RANUNI Routine
The following example
uses three different seeds and the CALL RANUNI routine to produce
multiple streams.
data uniform(drop=i);
seed1 = 255793849;
seed2 =1408147117;
seed3 = 961782675;
do i=1 to 10000;
call ranuni(seed1, x1);
call ranuni(seed2, x2);
call ranuni(seed3, x3);
i2 = lag(x2);
i3 = lag2(x3);
output;
end;
label i2='Lag(x2)' i3='Lag2(x3)';
run;
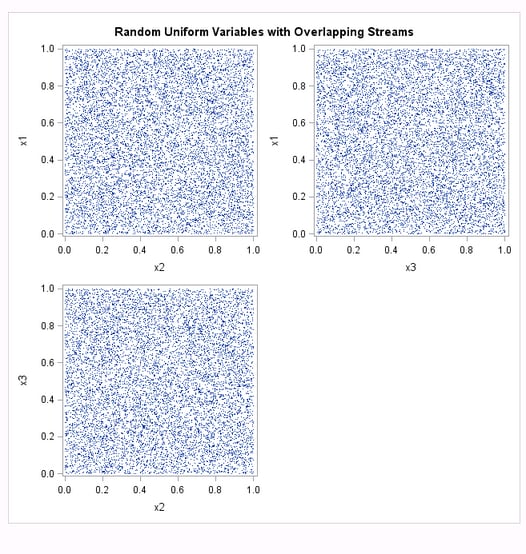
title 'Random Uniform Variables with Overlapping Streams';
proc sgscatter data=uniform;
plot x1*x2 x1*x3 x3*x2 / markerattrs = (size = 1);
run;
proc sgscatter data=uniform;
plot i2*x1 i3*x1 / markerattrs = (size = 1);
run;
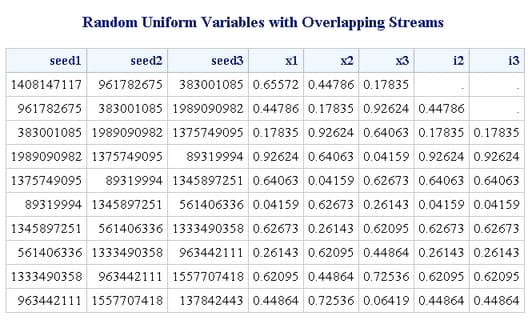
proc print noobs data=uniform(obs=10);
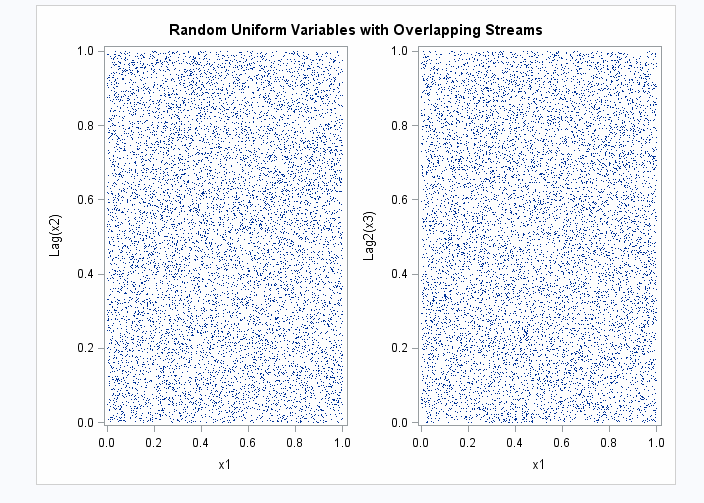
run;The first plot (
Using Different Seeds with CALL RANUNI: Random Uniform Variables with Overlapping Streams, Plot 1) shows expected results: the variables appear to be statistically
independent. However, the second plot ( Using Different Seeds with CALL RANUNI: Random Uniform Variables with Overlapping Streams, Plot 2) and the listing of the first 10 observations show that
there is almost complete overlap between the two streams. The last
9999 values in x1 match the first 9999 values in x2, and the last
9998 values in x1 match the first 9998 values in x3. In other words,
there is perfect agreement between the nonmissing parts of x1 and
lag(x2) and also x1 and lag2(x3). Even if the streams appear to be
independent at first glance as in the first plot, there might be overlap,
which might be undesirable depending on how the streams are used.
In practice, if you
make multiple small streams with separate and randomly selected seeds,
you probably will not encounter the problems that are shown in the
first two examples. Using Different Seeds with CALL RANUNI: Random Uniform Variables with Overlapping Streams, Plot 2 deliberately selects seeds to illustrate worst-case scenarios.
Generating Multiple Variables from One Seed in Random-Number Functions
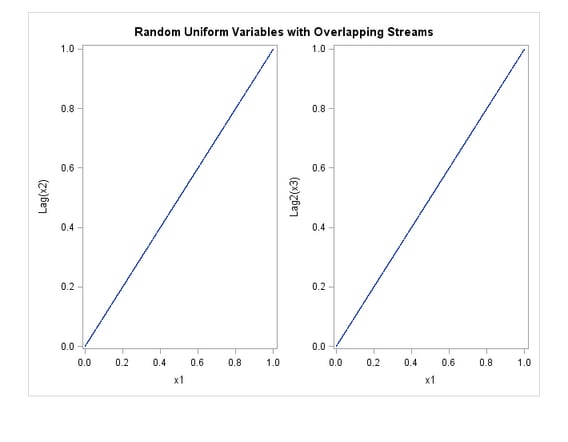
Example: Generating Random Uniform Variables with Overlapping Streams
In the following example,
the RANUNI function is used to create random uniform variables with
overlapping streams. The example shows the safest way to create multiple
variables by using the RANUNI function. All variables are created
from the same stream with a single seed.
data uniform(drop=i);
do i = 1 to 10000;
x1 = ranuni(11111);
x2 = ranuni(11111);
x3 = ranuni(11111);
i2 = lag(x2);
i3 = lag2(x3);
output;
end;
label i2 = 'Lag(x2)' i3 = 'Lag2(x3)';
run;
title 'Random Uniform Variables with Overlapping Streams';
proc sgscatter data = uniform;
plot x1*x2 x1*x3 x3*x2 / markerattrs = (size = 1);
run;
proc sgscatter data = uniform;
plot i2*x1 i3*x1 / markerattrs = (size = 1);
run; In Example: Generating Random Uniform Variables with Overlapping Streams, it appears that the variables are independent. However,
even this programming approach might not work well in general. The
random-number functions and CALL routines have a period of only 231 -
2 or less (approximately 2.1 billion). When this limit is reached,
the stream repeats. Modern computers performing complicated simulations
can easily exhaust the entire stream in minutes.
Using the RAND Function as an Alternative
A better approach to
generating random uniform variables is to use the RAND function, where
multiple streams are not permitted. The RAND function has a period
of 219937 - 1. This limit will never be
reached, at least with computers of the early 21st century. The number
219937 - 1 is approximately 106000 (1
followed by 6000 zeros). In comparison, the largest value that can
be represented in eight bytes on most computers that run SAS is approximately
10307.
The RAND function, which
is the latest random-number function that was designed, does not
allow multiple streams. The RAND function uses a different algorithm
from the random-number CALL routines, which enable you to create multiple
streams with multiple seeds. Because the state of the RAND process
cannot be captured by a single seed, you cannot stop and restart the
generator from its stopping point. Therefore, the RAND function allows
only a single stream of numbers, but it can be used to make multiple
streams, just as the RANUNI function can.
Effectively Using the Random-Number CALL Routines
Starting, Stopping, and Restarting a Stream
A reasonable use of
the random-number CALL routines is starting and stopping a single
stream, provided the stream never exhausts the RANUNI stream. For
example, you might want SAS to perform iterations, stop, evaluate
the results, and then restart the stream at the point that it stopped.
The following example illustrates this principle.
Example: Starting, Stopping, and Restarting a Stream
This example generates
a stream of five numbers, stops, restarts, generates five more numbers
from the same stream, combines the results, and generates the full
stream for comparison. In the first DATA step, the state of the random-number
seed is stored in a macro variable seed for use as the starting seed
in the next step. The separate streams in the example output match
the full stream.
data u1(keep=x);
seed = 104;
do i = 1 to 5;
call ranuni(seed, x);
output;
end;
call symputx('seed', seed);
run;
data u2(keep=x);
seed = &seed;
do i = 1 to 5;
call ranuni(seed, x);
output;
end;
run;
data all;
set u1 u2;
z = ranuni(104);
run;
proc print label;
title 'Random Uniform Variables with Overlapping Streams';
label x = 'Separate Streams' z = 'Single Stream';
run;Comparison of Changing the Seed in a CALL Routine and in a Function
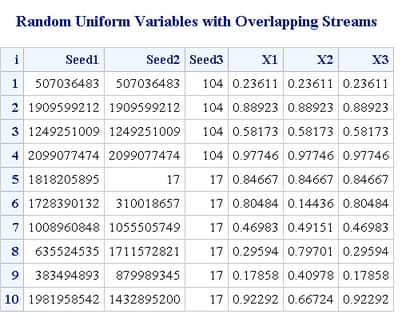
Example: Changing Seeds in a CALL Routine and in a Function
If you use a CALL routine
to change the seed, the results are different from using a function
to change the seed. The following example shows the difference.
data seeds;
retain Seed1 Seed2 Seed3 104;
do i = 1 to 10;
call ranuni(Seed1,X1);
call ranuni(Seed2,X2);
X3 = ranuni(Seed3);
if i = 5 then do;
Seed2 = 17;
Seed3 = 17;
end;
output;
end;
run;
proc print data = seeds;
title 'Random Uniform Variables with Overlapping Streams';
id i;
run;Copyright © SAS Institute Inc. All rights reserved.