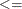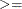Working with Matrices
Elementwise Binary Operators
Elementwise binary operators produce a result matrix from element-by-element operations on two argument matrices.
Table 5.2 lists the elementwise binary operators.
Table 5.2: Elementwise Binary Operators
|
Operator |
Description |
|---|---|
|
|
Addition; string concatenation |
|
|
Subtraction |
|
|
Elementwise multiplication |
|
|
Elementwise power |
|
|
Division |
|
|
Element maximum |
|
|
Element minimum |
|
| |
Logical OR |
|
|
Logical AND |
|
< |
Less than |
|
|
Less than or equal to |
|
> |
Greater than |
|
|
Greater than or equal to |
|
^= |
Not equal to |
|
= |
Equal to |
For example, consider the following two matrices:
![\[ \mb{A} = \left[ \begin{array}{rr} 2 & 2 \\ 3 & 4 \\ \end{array} \right], \mb{B} = \left[ \begin{array}{rr} 4 & 5 \\ 1 & 0 \\ \end{array} \right] \]](images/imlug_workmatrix0026.png)
The addition operator 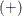 adds corresponding matrix elements, as follows:
adds corresponding matrix elements, as follows:
![\[ \mb{A} + \mb{B} \mbox{ is } \left[ \begin{array}{rr} 6 & 7 \\ 4 & 4 \\ \end{array} \right] \]](images/imlug_workmatrix0028.png)
The elementwise multiplication operator 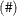 multiplies corresponding elements, as follows:
multiplies corresponding elements, as follows:
![\[ \mb{A} \# \mb{B} \mbox{ is } \left[ \begin{array}{rr} 8 & 10 \\ 3 & 0 \\ \end{array} \right] \]](images/imlug_workmatrix0030.png)
The elementwise power operator 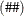 raises elements to powers, as follows:
raises elements to powers, as follows:
![\[ \mb{A} \# \# 2 \mbox{ is } \left[ \begin{array}{rr} 4 & 4 \\ 9 & 16 \\ \end{array} \right] \]](images/imlug_workmatrix0032.png)
The element maximum operator 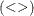 compares corresponding elements and chooses the larger, as follows:
compares corresponding elements and chooses the larger, as follows:
![\[ \mb{A} <> \mb{B} \mbox{ is } \left[ \begin{array}{rr} 4 & 5 \\ 3 & 4 \\ \end{array} \right] \]](images/imlug_workmatrix0034.png)
The less than or equal to operator 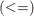 returns a 1 if an element of
returns a 1 if an element of 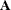 is less than or equal to the corresponding element of
is less than or equal to the corresponding element of 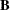 , and returns a 0 otherwise:
, and returns a 0 otherwise:
![\[ \mb{A} <= \mb{B} \mbox{ is } \left[ \begin{array}{rr} 1 & 1 \\ 0 & 0 \\ \end{array} \right] \]](images/imlug_workmatrix0038.png)
All operators can work on scalars, vectors, or matrices, provided that the operation makes sense. For example, you can add
a scalar to a matrix or divide a matrix by a scalar. For example, the following statement replaces each negative element of
the matrix x with 0:
y = x#(x>0);
The expression x>0 is an operation that compares each element of x to (scalar) zero and creates a temporary matrix of results; an element of the temporary matrix is 1 when the corresponding
element of x is positive, and 0 otherwise. The original matrix x is then multiplied elementwise by the temporary matrix, resulting in the matrix y. To fully understand the intermediate calculations, you can use the RESET statement
with the PRINTALL option to have the temporary result matrices displayed.