Working with Matrices
Simple Assignment Statements
Simple assignment statements involve an equation that has a matrix name on the left side and either an expression or a function that generates a matrix on the right side.
Suppose that you want to generate some statistics for the weekly coffee data. If a cup of coffee costs 30 cents, then you
can create a matrix with the daily expenses, dayCost, by multiplying the per-cup cost with the matrix coffee. You can turn off the automatic printing so that you can customize the output with the ROWNAME=, FORMAT=, and LABEL= options
in the PRINT statement, as shown in the following statements:
reset noprint; dayCost = 0.30 # coffee; /* elementwise multiplication */ print dayCost[rowname=names format=8.2 label="Daily totals"];
Figure 5.5: Daily Cost for Each Employee
You can calculate the weekly total cost for each person by using the matrix multiplication operator (*). First create a 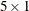 vector of ones. This vector sums the daily costs for each person when multiplied with the
vector of ones. This vector sums the daily costs for each person when multiplied with the coffee matrix. (A more efficient way to do this is by using subscript reduction operators, which are discussed in the section Using Matrix Expressions.) The following statements perform the multiplication:
ones = {1,1,1,1,1};
weektot = dayCost * ones; /* matrix-vector multiplication */
print weektot[rowname=names format=8.2 label="Weekly totals"];
You might want to calculate the average number of cups consumed per day in the office. You can use the SUM function, which
returns the sum of all elements of a matrix, to find the total number of cups consumed in the office. Then divide the total
by 5, the number of days. The number of days is also the number of columns in the coffee matrix, which you can determine by using the NCOL function. The following statements perform this calculation:
grandtot = sum(coffee);
average = grandtot / ncol(coffee);
print grandtot[label="Total number of cups"],
average[label="Daily average"];
Figure 5.7: Total and Average Number of Cups for the Office